123 ceaser I: Podstawą ostrosłupa ABCS jest trójkąt prostokątny ABC, którego przeciwprostokątna AB ma 26 cm długości, a przyprostokątna AC ma 24 cm długości. Krawędź SA jest prostopadła do płaszczyzny podstawy ABC, |SA|=18 cm. Oblicz pole powierzchni bocznej ostrosłupa

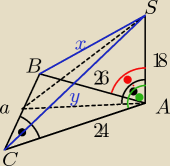
Thor: Ppb= P_CAS + P+_BAS + P_CSB a=√26² − 24 2=10 P_CAS = 24*18/2 = 216 P_BAS= 26*18/2=234 x=√576+324=30 y=√676+324=10√10 p=Ob/2=40+10√10/2= 20+5√10 P_CBS= p{20+5√10*(10+5√10)*(5√10−10)*(20−5√10) = √150²= 150 v (−150 − odrzucamy) Ppb= 600.

Thor: poprawki w zapisie: a=√26² − 24²=10 p=Ob/2=40+10√10/2= 20+5√10 − p ze wzoru na pole trojkata majac boki P=√p(p−a)(p−b)(p−c) PCBS= √20+5√10*(10+5√10)*(5√10−10)*(20−5√10) = √1502= 150 v (−150 − odrzucamy)