pomocy atenka: jak mozna to z wyjaśnieniem proszę Oblicz objetość i pole powierzchni całkowitej prawidłowego ostrosłupa trójkątnego, którego krawędź podstawy ma 10 cm długości, a kąt dwuścienny między ścianą boczną a podstawą ma miarę 60 stopni.

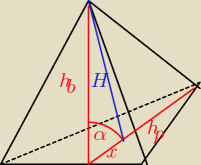Basia: α=60

	a2√3		102√3		100√3
Pp =		=		=		= 25√3
	4		4		4

	a√3		10√3
hp =		=		= 5√3
	2		2

	1		5√3
x =		hp =
	3		3

	H
tgα=
	x

	H
tg60 =
	x

H = x*tg60 podstaw i wylicz H

	1
V =		*Pp*H
	3

	x
cosα =
	hb

	x
cos60 =
	hb

	x
hb =
	cos60

podstaw i wylicz h_b

	1
Pściany =		*a*hb
	2

P_c = P_p+3*P_ściany

Janusz Sprytny Bystry: Δγ≈≈

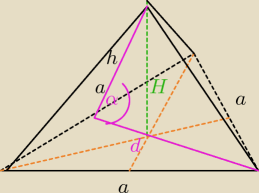U: α = 60 a = 10

	a√3
d=		− wyliczamy d
	2

Następnie zauważamy twójkąt prostokątny między wysokością ostrosłupa a U{1}/{3} wysokości podstawy.

	1
Wyliczamy tangensem wysokośc H. Obliczamy objętośc V=		* Pp * H.
	3

Wyliczamy wysokość ściany bocznej tym samym tangensem, albo już Pitagorasem. Potem liczyby pole

	1
tego trójąta i używamy wzoru na pole Δ, czyli P=		* a * h
	2

ceaser I: https://matematykaszkolna.pl/forum/83559.html a to dacie rade policzyc ? bo sie w pewnym momencie zaciąłem