| 1 | ||
\alpha = | obraca się wokół krótszej podstawy DC a) Sporządź rysunek powstałej bryły i | |
| 4 |
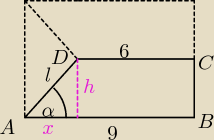 x = 9−6 = 3
xl = cos α = 14
l = 4x = 4*3 = 12
h = √l2−x2 = √122−32 = √135
Objętość powstałej bryły = objętość walca − objętość stożka
objętość walca o promieniu r = h =√135 i wysokości 9
Vw = πr2*h = π*(√135)2*9 = 1215π
objętość stożka o promieniu r = h = √135 i wysokości x = 3
Vs = 13πr2*x = 13π(√135)2*3 = 135π
objętość bryły
Vb = Vw − Vs = π(1215−135) = 1080π cm3
Powierzchnia powstałej bryły = pow podst walca + pow boczna walca + pow boczna stożka
Pb = πr2 + 2πr*9 + πrl = π[(√135)2*9 + 2*√135*9 + r*l] = π(1215+18√135+12√135) =
= (30√135 + 1215)π cm2
jak taką bryłe nazwać ? nie wiem
x = 9−6 = 3
xl = cos α = 14
l = 4x = 4*3 = 12
h = √l2−x2 = √122−32 = √135
Objętość powstałej bryły = objętość walca − objętość stożka
objętość walca o promieniu r = h =√135 i wysokości 9
Vw = πr2*h = π*(√135)2*9 = 1215π
objętość stożka o promieniu r = h = √135 i wysokości x = 3
Vs = 13πr2*x = 13π(√135)2*3 = 135π
objętość bryły
Vb = Vw − Vs = π(1215−135) = 1080π cm3
Powierzchnia powstałej bryły = pow podst walca + pow boczna walca + pow boczna stożka
Pb = πr2 + 2πr*9 + πrl = π[(√135)2*9 + 2*√135*9 + r*l] = π(1215+18√135+12√135) =
= (30√135 + 1215)π cm2
jak taką bryłe nazwać ? nie wiem

