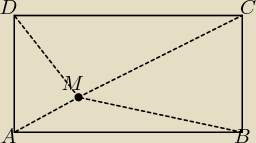
 Punkt M leży wewnątrz prostokąta ABCD (zob. rysunek).
Udowodnij, że AM2 + CM2 = BM2 + DM2.
Ciekawe zadanie, tylko jak to wykazać?
Punkt M leży wewnątrz prostokąta ABCD (zob. rysunek).
Udowodnij, że AM2 + CM2 = BM2 + DM2.
Ciekawe zadanie, tylko jak to wykazać?

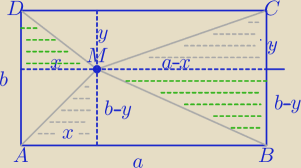 AM2 + CM2=BM2 + DM2.
1)
|AM|2=x2+(b−y)2
|CM|2=y2+(a−x)2
===========
AM|2 + |CM|2=x2+y2+(b−y)2+(a−x)2
2)
|BM|2 + |DM|2=(a−x)2+(b−y)2+x2+y2
3)
x2+y2+(b−y)2+(a−x)2=(a−x)2+(b−y)2+x2+y2
==================================
AM2 + CM2=BM2 + DM2.
1)
|AM|2=x2+(b−y)2
|CM|2=y2+(a−x)2
===========
AM|2 + |CM|2=x2+y2+(b−y)2+(a−x)2
2)
|BM|2 + |DM|2=(a−x)2+(b−y)2+x2+y2
3)
x2+y2+(b−y)2+(a−x)2=(a−x)2+(b−y)2+x2+y2
==================================