jeśli jest ktoś kto może pomóc..:)
Mikołaj:
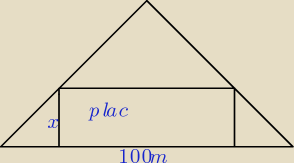
Działka ma kształt trójkąta równoramiennego o podstawie 100m i wysokości opuszczonej na tą
podstawę równej 50m. Właściciel działki chce wydzielić prostokątny plac o największym polu
powierzchni w sposób przestawiony na rysunku.
a) Oznacz szerokość wydzielonego terenu przez x[m] i zapisz wzór na pole P powierzchni placu w
zależności od x. Określ dziedzinę funkcji P
b) Wykaż że pole powierzchni placu jest największe wówczas, gdy jego wymiary wynoszą 25m na 50m
5 mar 11:09
Kacper18:
10 mar 19:50
Może ktoś zerknąc???:
10 mar 19:52
Może ktoś zerknąc???: Ma ktoś pomysł jak zacząć

?
10 mar 19:54
Vizer: spróbuje Ci pomóc, ale moga byc drobne błedy bo zaczynam dopiero pomagać, ale pomysł wydaje mi
się dobry

10 mar 20:18
Mikołaj: No było by super bo ja to nie mam żadnego pomysłu:(
10 mar 20:19
Vizer:
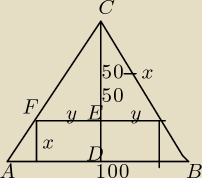
ΔADC∼ΔFEC (kk)
y=50−x
z=2y=100−2x
P=(100−2x)*x
D= (0,50)
Narazie masz a) zaraz bedzie b) sprawdz sobie czy dobrze rozumuje
10 mar 20:37
Vizer: b) P=−2x
2 +100x
Parabola ma ramiona skierowane w dol wiec wierzcholek paraboli przyjmuje wartość największą.
Więc liczymy x
w:
x
w=25[m]
Teraz liczymy drugą długość prostokąta [c[z]:
z=100−2x=100−2*25=50[m]
Wiec jak widzisz pole bedzie najwieksze dla 25 i 50 .
10 mar 20:44
Mikołaj: ok dzięki wielkie a jeszcze jedno jak można?
a to: ,,Oznacz szerokość wydzielonego terenu przez x[m,, gdzie to jest?
10 mar 20:57
Vizer: to jest to co sam zaznaczyles na rysunku szerokosc dzialki
10 mar 21:18
Mikołaj: aha

no racja
jak się kiedyś może spotkamy to masz u mnie piwo

10 mar 21:24
Mikołaj: miało byc ostatnie pytanie ale jeszcze jedno. skąd wiadomo że dziedzina jest od 0 do 50?
10 mar 21:25
Vizer: wieksze 0 dlatego, ze dlugosci bokow sa dodatnie, mniejsze 50 bo wysokosc trojkata jest rowna
50m wiec wysokosc prostokata nie moze byc wieksza

10 mar 21:28
 Działka ma kształt trójkąta równoramiennego o podstawie 100m i wysokości opuszczonej na tą
podstawę równej 50m. Właściciel działki chce wydzielić prostokątny plac o największym polu
powierzchni w sposób przestawiony na rysunku.
a) Oznacz szerokość wydzielonego terenu przez x[m] i zapisz wzór na pole P powierzchni placu w
zależności od x. Określ dziedzinę funkcji P
b) Wykaż że pole powierzchni placu jest największe wówczas, gdy jego wymiary wynoszą 25m na 50m
Działka ma kształt trójkąta równoramiennego o podstawie 100m i wysokości opuszczonej na tą
podstawę równej 50m. Właściciel działki chce wydzielić prostokątny plac o największym polu
powierzchni w sposób przestawiony na rysunku.
a) Oznacz szerokość wydzielonego terenu przez x[m] i zapisz wzór na pole P powierzchni placu w
zależności od x. Określ dziedzinę funkcji P
b) Wykaż że pole powierzchni placu jest największe wówczas, gdy jego wymiary wynoszą 25m na 50m
 ?
?

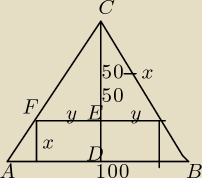 ΔADC∼ΔFEC (kk)
ΔADC∼ΔFEC (kk)
 no racja
jak się kiedyś może spotkamy to masz u mnie piwo
no racja
jak się kiedyś może spotkamy to masz u mnie piwo
