planimetria karolina: W rozwartokatnym trójkącie równoramiennym ABC ( |AC|=|BC| ) odległość środka koła wpisanego w trójkąt od wierzchołka A jest równa d, a |∠ACB|=2α. Oblicz pole trojkata ABC i promien koła opisanego na trojkacie ABC.

Godzio:

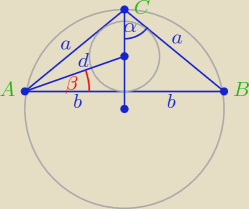
	90 − α		1
β =		= 45 −		α
	2		2

	1		b		1
cos(45 −		α) =		⇒ b = d * cos(45 −		α)
	2		d		2

	b		b		1   d * cos(45 − α)   2
sinα =		⇒ a =		⇒ a =
	a		sinα		sinα

Z tw. sinusów:

2b		b		1   d * cos(45 − α)   2
	= 2R ⇒ R =		⇒ R =
sin2α		sin2α		sin2α

	1		1		1   d2 * cos2(45 − α)   2
P =		a2sin2α =		*		* 2sinαcosα =
	2		2		sin2α

	1
= d2 * cos2(45 −		α) * ctgα
	2

Odp:

	1   d * cos(45 − α)   2		1
R =		, P = d2 * cos2(45 −		α) * ctgα
	sin2α		2