Oblicz pole ograniczne liniami Olaf: Pole ograniczone liniami y = 4 − x⁴ i y = 0 Obliczyc całke ∫(3−e^−x)dx Posze o pomoc

Godzio: x⁴ = 4 ⇒ x = √2 lub x = −√2 Wykres jest parzysty więc wystarczy policzyć pole: ^√2₀∫(4− x⁴)dx i pomnożyć przez 2

	x5
... = 2 * (4x −		)|√20 = ...
	5

∫(3 − e^−x)dx = 3x + e^−x + C

Olaf: a moze ktos wytlumaczyc dlaczego tak to pierwsze bo nie wiem o co za bardzo chodzi

Godzio: Ale co dokładnie, czego nie wiesz ?

Olaf: jak wgl to pole obliczyc i skad wziales ten wzor na calke

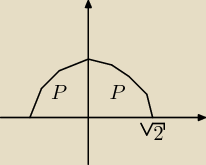
Godzio: Tak normalnie się liczy Tak miej więcej wygląda wykres, oczywiście narysowałem tą część która nas interesuje, Obie strony mają równe Pole więc zapisujemy:

	x5
√20∫(4 − x4)dx, wynikiem całki jest 4x −		+ C i teraz licząc całkę oznaczoną
	5

wstawiamy górną granicę całkowania:

	4√2		0
4√2 −		i dolną, tutaj wszystko się wyzeruje 4 * 0 −		, więc otrzymujemy pole
	5		5

	4
jednej częśći:		* 4√5, nam chodzi o całość więc mnożymy przez 2 ⇒
	5

	16√5		32√5
Pc = 2 *		=
	5		5

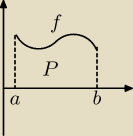
Godzio: P = ^a_b∫f(x)dx = Φ(a) − Φ(b) gdzie Φ'(x) = f(x)

Olaf: stary wielkie dzieki a potrafisz obliczyc ekstrema loklalne funkjci z = xy − x² − y² + x bo z abardzo tego tez nie kumam

Godzio: Tego jeszcze nie umiem

Olaf: a mozesz mi powiedziec skad jest 4√2 po podstawieniu √2 do x⁵ i dlaczego pozniej jest 4/5 * 4√5

Godzio: x⁵, x = √2 ⇒ √2⁵ = √2 * √2 * √2 * √2 * √2 = 2 * 2 * √2 = 4√2 4√2 = jabłko

	1		4
1 jabłko −		jabłka =		jabłka, sory że tak to tłumacze, ale tak chyba najłatwiej
	5		5

zrozumieć

Godzio: √5 napisałem przez przypadek, pewnie o to chodziło

Olaf: ale czemu 4√5 o to bardziej mi chodzi

Olaf: dobra teraz jeszcze jednen problem najmniejsza i najwiekasza wartosc funkcji f(x) = x³ − 3x +1 na przedziale [−1;4] wiem ze trzeba policzyc f(−1) i f(4) tylko cos mi tu nie pasuje

Godzio: Policz pochodną i ekstrema i wtedy f(−1) f(4) f(ekstremów) i wybierz największą i najmniejszą wartość

Godzio: f'(x) = 3x² − 3x 3x² − 3x = 0 ⇒ 3x(x − 1) = 0 ⇒ x = 1 lub x = 0, pochodna zmienia znak w tych punktach więc policz f(−1) = ... f(4) = ... f(1) = ... f(0) = ... I podaj odpowiedź

Olaf: czyli tak f'(x) = 3x² − 3 3x² − 3 =0 3x² = 3 x² = 1 x=1 i x=−1 u gory rys do tego i co dalej ?

Godzio: A widzę że walnąłem się w pochodnej , teraz liczysz f(1), f(−1), f(4) i znajdź te max i min

Olaf: a pamietasz kiedy bylo min a kiedy max ? −na + bym max czy min? xD nei pamietam tego xD

Godzio: Z + na − ⇒ funkcja rośnie, dochodzi do ekstremum i zaczyna maleć ⇒ jest to maksimum Z − na + ⇒ funkcja maleje, dochodzi do ekstremum i zaczyna rosnąć ⇒ i to jest minimum

Olaf: f(1) = 1 −3 +1 = −1 f(−1) = −1 +3 +1 = 3 f(4) = 64 − 12 +1 = 53 i co dalej ? xD

Godzio: Wartość maksymalna 53 minimalna −1

Olaf: czyli fmax = f(−1) = 3 fmin = f(1) = −1 i to wszystko ?

Godzio: Tak by było gdyby nie było tej 4, ale skoro ją mamy więc wartość dla 4 też wliczamy

Olaf: ok wielkie dzieki

Trivial: f(x, y) = xy − x² − y² + x. f(x, y) ∊ C^∞(R²), czyli ekstremum lokalne musi być w miejscu, gdzie ∇f = 0.

∂f
	= y − 2x + 1.
∂x

∂f
	= x − 2y.
∂y

⎧	y −2x − 1 = 0
⎩	x − 2y = 0

	2		1
x =		y =
	3		3

	2		1
P0 = (		,		) − kandydat na ekstremum lokalne.
	3		3

∂2f
	= −2.
∂x2

∂2f
	= 1.
∂x∂y

∂2f
	= −2.
∂y2

	−2 1 1 −2
Hf(P0) =

A₁ = det(−2) = −2 < 0

	−2 1 1 −2
A2 = det		= 4 − 1 = 3 > 0

	2		1
Wniosek: Punkt P0 = (		,		) to maksimum lokalne.
	3		3