romby Agula: Bok rombu ma długość 4 cm, a suma długości jego przekątnych jest równa 10 cm. Oblicz pole i wysokość tego rombu

Kaśka: Jeżeli narysujemy romb i zaznaczymy przekątne oraz bok a = 4 to otrzymamy 4 trójkąty prostokątne. Przekątne e podzielona będzie na dwa odcinki x i x, a przekątna f na y i y Z twierdzenia pitagorasa mozemy obliczyć połowę przekątnej e i f x² + y² = 4² x² + y² = 16 Suma przekątnych jest równa 10 cm, czyli 2x + 2y = 10 /: 2 x + y = 5 Mamy dwa równania, liczymy układ równań: x + y = 5 x² + y² = 16 x = 5 − y (5 − y)² + y² = 16 x + y = 5 25 − 10y + y² + y² = 16 x + y = 5 2y² − 10y + 25 − 16 = 0 x + y = 5 2y² − 10y + 9 = 0 Liczymy pierwiastki z II równania: Δ = b² − 4ac = 100 − 72 = 28 √Δ = √28 = √4*7 = 2√7 x₁ = (−b − √Δ) : 2a = (10 − 2√7 ) : 4 = 2(5 − √7) : 4 = (5 − √7)/2 x₂ = (−b + √Δ) : 2a = (10 + 2√7 ) : 4 = 2(5 + √7) : 4 = (5 + √7)/2 x1 = x x₂ = y e = 2 x = 2 * (5 − √7)/2 = (5 − √7) f = 2y = 2 * (5 + √7)/2 = (5 + √7) Liczymy pole: P = (e * f)/ 2 = [(5 − √7)*(5 + √7)] : 2 = ( 25 − 7) : 2 = 18 :2 = 9 Wysokość: P = a * h h = P/a h = 9cm²/ 4 cm h = 2, 25cm Odp Pole rombu wynosi 9 cm², a wysokość ma 2,25cm

Bogdan:

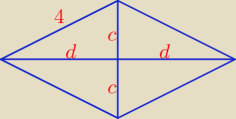
	1
Pole rombu P =		*2c*2d = 2cd
	2

c² + d² = 16 i 2c + 2d = 10 ⇒ c + d = 5 (c + d)² = c² + 2cd + d² ⇒ 5² = 16 + P ⇒ P = 9

	9
P = 4*h (h to wysokość rombu), 9 = 4*h ⇒ h =
	4

Agula: dzięki