Wyznacz zbiór wartości funkcji Mary: Wyznacz zbiór wartości funkcji f(x)=3−4sinx−4cos²x Tam potem wychodzi mi 4t²−4t−1 po podstawieniu za sinx, ale co dalej z tym zrobić?

Mzmuda1995: f(x)=3−4sinx−4cos²x=3−4sinx−4(1−sin²x)=4sin²x−4sinx−1=(2sinx−1)²−2 −1<=sinx>=1 najmniejsza wartość wyrażenia (2sinx−1)² jest równa 0 gdyż x²>=0, więc najmniejsza wartość funkcji to −2 natomiast największa wartość wyrażenia (2sinx−1)² jest równa 9 (dla sinx=−1), więc największa wartość funkcji to 7 Zatem zb∊<−2;7> Mam nadzieję, że pomogłem

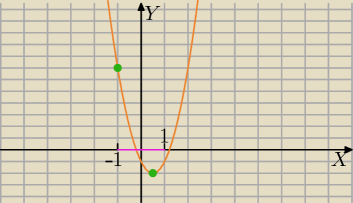
Mila: f(t)= 4t²−4t−1 i t∊<−1;1> a=4 parabola skierowana do góry wartość najmniejsza f(t) w wierzchołku tej paraboli

	−b		4		1
tw=		=		=		∊<−1;1>
	2a		8		2

	1		1		1
zatem f(		)=4*		−4*		−1=−2
	2		4		2

Największą obliczymy na końcach przedziału f(−1)=7 f(1)=−1

Mila: Oczywiście daj odpowiedź.