| q2 | p3 | |||
Δ= | + | |||
| 4 | 27 |
| (−1)2 | (−3)3 | 1 | 3 | |||||
Δ= | + | = | −1=− | <0 | ||||
| 4 | 27 | 4 | 4 |
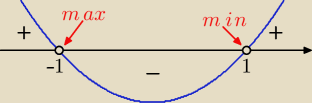 albo: f(x) = x3 − 3x − 1, f '(x) = 3x2 − 3 = 3(x + 1)(x − 1)
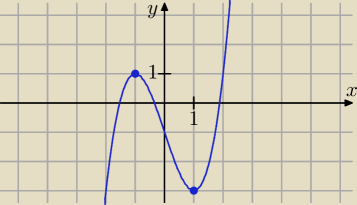
f '(x) = 0 dla x = −1 lub x = 1, f(−1) = 1, f(1) = −3,
funkcja ma 2 ekstrema: maksimum w punkcie (−1, 1), minimum w punkcie (1, −3),
zatem ma 3 miejsca zerowe, a równanie x3 − 3x − 1 ma 3 pierwiastki.
albo: f(x) = x3 − 3x − 1, f '(x) = 3x2 − 3 = 3(x + 1)(x − 1)
f '(x) = 0 dla x = −1 lub x = 1, f(−1) = 1, f(1) = −3,
funkcja ma 2 ekstrema: maksimum w punkcie (−1, 1), minimum w punkcie (1, −3),
zatem ma 3 miejsca zerowe, a równanie x3 − 3x − 1 ma 3 pierwiastki.