obrotowe
Aniusia: proszę pomóżcie. Dwusieczna kąta prostego w trójkącie prostokątnym o przeciwprostokątnej =35cm
dzieli tą przeciwprostokątną w stosunku 3/4. Oblicz pole powierzchni bryły otrzymanej z obrotu
danego trójkąta wokół przeciwprostokątnej.
28 lut 21:44
Aniusia: proszę pomóżcie. Dwusieczna kąta prostego w trójkącie prostokątnym o przeciwprostokątnej =35cm
dzieli tą przeciwprostokątną w stosunku 3/4. Oblicz pole powierzchni bryły otrzymanej z obrotu
danego trójkąta wokół przeciwprostokątnej.
28 lut 21:56
jo:
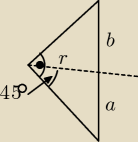
Rozwiąż pierwsze ten układ dwóch równań:
a+b = 35
Pytaj jak nie będziesz wiedziała skąd co się bierze...
28 lut 22:08
Pomocy-Proszę: ja nie bardzo to umiem
proszę zrób mi całe zadanko
a jutro jak byś miał czas to trochę mi
potłumaczysz z obrotowych ok?
plissssss
28 lut 22:18
jo: Wolałabym jednak abyś coś obliczyła...
Rozwiązaniem będzie: a=15, b=20
Teraz sobie narysuj bryłę która powstanie przez obrót wokół przeciwprostokątnej − będą to dwa
stożki złączone ze sobą podstawami...
28 lut 22:29
jo: Jestem już zmęczona i naprawdę nie mam już dzisiaj siły tyle pisać i rysować...
28 lut 22:32
Gustlik: Jo, a nie można prościej − bez układu równań?
| | a | | 3 | |
Skoro |
| = |
| , to a=3x, b=4x
|
| | b | | 4 | |
Mamy więc 3x+4x=35
7x=35 /:7
x=5
a=3*5=15
b=4*5=20.
Skorzystam z rysunku Jo, bo u mnie rysowanie zawiesza kompa.
Teraz nazwijmy sobie a' przyprostokątną odpowiadającą odcinkowi a wyciętemu przez dwusieczną, a
więc "dolną" przyprostokątna i analogiczbie b' − "górną" przyprostokatna.
Zgodnie z twierdzeniem o dwusiecznej trójkąta (
https://matematykaszkolna.pl/strona/498.html ) mamy:
| a' | | a | | 3 | |
| = |
| = |
| , zatem a'=3y, b'=4y
|
| b' | | b | | 4 | |
Z tw. Pitagorasa mamy:
(3y)
2+(4y)
2=35
2
9y
2+16y
2=1225
25y
2=1225 /:25
y
2=49 /
√
y=7
Zatem a'=3*7=21, b'=4*7=28
Bryła powstała z obrotu tego trójkąta to bedą dwa stożki złączone podstawami o tworzących
l
1=a'=21 i l
2=b'=28
Potrzebny jest jeszcze promień podstawy − będzie to wysokość opuszczona z wierzchołka kąta
prostego na przeciwprostokątną.
Obliczę to z pola liczonego na dwa sposoby.
| | 1 | | 1 | |
P= |
| a'b'= |
| *21*28=21*14=294
|
| | 2 | | 2 | |
Teraz pole liczone z przeciwprostokątnej jako podstawy i wysokości h opuszczonej z wierzchołka
kąta prostego:
35h=588 /:35
h=16,8=r − promień wspólnej podstawy
Pole powierzchni bocznej stożka P=πrl, gdzie r − promień podstawy, l − tworząca
Zatem
P=πra'+πrb'=πr(a'+b')=π*16,8*(21+28)=π*16,8*49=823,2π
Odp. P=823,2π cm
2.
1 mar 01:45
komentator OWMH:
uwaga 1: aby rozwiązać r−nie y
2 = 49 nie stosuje się
√ po obie stronie
to są błędy popełnione przez uczniów w podstawówce i gimnazjum i się ciągnie
nie wiadomo do kiedy, to błędy są przeoczone przez nauczycieli.
r−nie y
2 = 49 (r−nie drugiego stopnia) ona jest równoważna do y
2−49=0
prawa strona da się zapisać w postaci iloczynowej ( y−7) (y+7) = 0
stąd y
1=7 lub y
2=−7 ponieważ długości odcinków wyrażone liczbami dodatnimi
to y jest dodatni a więc y
1=7 jest rozwiązaniem równania y
2=49.
A TERAZ NA SERIO:
PIERWSZA RECZ JEST DOWIEDZIEĆ SIĘ CO JEST NAM POTZREBNE Z RYSUNKU
WYKONANE PRZEZ NASZ (PO PRZECZYTANIU TREŚCI ZADANIA)
1.− PO OBROTU TRÓJKĄTA DOOKOŁA PRZECIWPROSTOKĄTA OTRZYMAMY DWIE
STOŻKI PRZYKLEJONYCH PRZEZ SIEBIE PRZY PODSTAWIE O PROMIENIU R
TZN. ŻE KAŻDY Z STOŻEK MA PODSTAWA O PROMIENIU R I TWORZACA BĘDĄCA
JEDNA Z PRZYPROSTOKĄTA
A TERAZ ROBIMY ANALIZA TEGO ZADANIA ABY ZNALEŻĆ CO JEST NAM POTRZEBNE
DO ROZWIAZANIA NASZEGO ZADANIA
2.− POLE POWIERZCHNI TEJ FIGURY OTRZYMANEJ = SUMA POLE BOCZNE TYCH STOŻEK
P
fig = P
bocznej stożek 1 + P
bocznej stożek 2
P
bocznej stożek = π R L ; gdzie R − długość promienia podstawy stożka
L − długość tworzącej stożka
NASZE OZNACZENIE a' długość jednej z przyprostokątne a długości drugiej b'
P
fig = π R a' + π R b'
P
fig = π R (a' + b')
a więc trzeba znaleźć długości przyprostokątne: a' i b'
3.− jak znaleźć R
R z rysunku to odcinek prostopadły do przeciwprostokątnej inaczej to wysokość
odpowiadającej tej przeciwprostokątnej.
Bok i odpowiedniej jej wysokości zasugeruje posługiwanie się pojęcią pole trójkąta
ponieważ nasz trójkąt jest prostokątny mamy dwa sposoby obliczenia tego pola
po pierwsze:
P
trójkąta =
35 R2 ( inaczej P
trójkąta =35R:2)
po drugie: biorąc pod uwagę ze trójkąt jest prostokątny tzn. że a' jest wysokością
odpowiadające b' i wice versa
P
trójkąta =
a'.b' 2 ( inaczej P
trójkąta = a' . b' : 2 )
a więc mamy że R =
a'.b'35 (inaczej R = a'. b': 35)
z punktów 1 i 2 mamy że
P
fig =
π a'.b' (a' + b') 35 ( inaczej P
fig = π a'.b' (a' + b'):35)
uwaga 2 :
Postać twierdzeń i definicji w matematyce mają swoje interpretacji warto sie
nauczyć to żeby można było zapamiętać bez trudu i wysłowić jego treści
TW o dwusiecznej w trójkącie mówi że dwusieczna dowolnego kąta w trójkącie
dzieli jego przeciwległy boku na dwie części które są wprost proporcjonalne
do odpowiednich dwóch pozostałych boków ( bo dwusieczna dziele trójkąt na
dwie części a więc jeden z boków tego kąta (dzielonego przez tę dwusieczną )
i jeden z odcinków otrzymany na przeciwległej boku tego kąta po wprowadzeniu
tej dwusieczni leżą po tej samej stronę w stosunku do tej dwusieczni).
Dla naszego zadania oznaczyłby że:
jeśli a' i b' są bokami tworzące kata dzielone przez tę dwusieczną również
a i b są odpowiednimi ich odcinków wyznaczonych na przeciwległym boku
wymienionego kąt, to znaczy że a' i a leżą po tej samej strony po
dzieleniu trójkąta przez tę dwusieczną na dwie części, również b' i b
ich długościami można wyrazić następująco; wiedząc że a jest w
relacji z b tak jak 3:4 również a" jest w relacji z b' tak jak 3:4 a więc
mamy że:
Po pierwsze a = 3r i b = 4r również a + b= 35
rozwiązując pierwsze układ równań mamy r= 5 stąd a=15 i b=20
(nie potrzebne rozwiązać tego układu , wiadomo dlaczego tak
)
A teraz co jest ważne dla rozwiązania naszego zadania
!
Po drugie a' = 3t i b' = 4t również
(a')
2 + (b')
2 = 35
2 (z twierdzenia Pitagorasa bo a' i b'
z treści zadania są przyprostokątnymi a 35 jest długością
przeciwprostokątnej)
Z DRUGIEGO UKŁADU R−NAŃ : mamy t=7, stąd a'= 21 [cm] i b'=28 [cm]
a więc podstawiając w : P
fig = π a'. b' (a' + b') to mamy:
P
fig = π 21 . 28 . (21 + 28) : 35
P
fig = π 3. 28.49:5
P
fig = π 3. 28.49.2 : (5.2)
P
fig = π 6. 4. 7.49. : 10
P
fig = 823,2 π [cm
2]
A WIĘC PODSTAWOWE ZASAD PRZY ROZWIĄZYWANIU ZADAŃ Z MATEMATYKI
1.− CZYTAĆ TREŚĆ ZADANIA I ZROZUMIEĆ POLECENIE
2.− WYKONAĆ RYSUNEK POTRZEBNE DO OGARNIĘCIA W UJĘCIU GLOBALNYM TEGO
PROBLEMU. ( ZROZUMIEĆ W CAŁOŚĆI)
( POTRZEBNE NAM ABY MIEĆ POJECIA Z CZYM MAMY DO CZYNIENIA)
3.− ZROBIĆ DODATKOWYMI ANOTACJI POTRZEBNYCH DO USTALENIE NASZYCH DANYCH
I SZUKANYCH WIELKOŚCIACH.
4.− SZUKAĆ W TRZEŚCI POTRZEBNE OKREŚLEŃ MATEMATYCNYCH ABY PRZYPOMIEĆ
DEFINICJI, TWIERDZEŃ , WZORÓW , .. ITD.I STOSOWAĆ ODPOWIEDNYCH ICH .
ZA RAZEM STOSOWAĆ PRAWE, REGUŁY, METODY KTÓRE DOPROWADZĄ DO
ZNALEZENIE TYCH POŚREDNICH, WIELKOŚCI POTRZEBNE DO ROZWIĄZYWANIA
TEGO ZADANIA.
TU RÓWNIEZ USTALAMY JAK I OD CZEGO ZALEŻY TĘ WIELKOŚIĄ SZUKANĄ; PISZĄC
ODPOWIEDNI WZÓR (RELACJĘ POMIĘDZY TYCH POŚREDNICH WIELKOŚCI A Z TĄ
SZUKANĄ)
5.− PUNKTÓW 1 − 4 DOPROWADZAJĄ DO ROZDROBNIENIA TEGO PROBLEMU NA
KAWAŁKACH, KTÓRYCH BĘDĄ ANALIZOWANE (OBLICZONE) OSOBNO ŻEBY
W KOŃCU POWRACAĆ DO TEGO CO MY SZUKAMY.
6.− PRZY OBLICZENIACH (RACHUNKÓW) WARTO PAMIĘTAĆ, ŻE NIE OBLICZAMY
MECHANYCZNE , TZN.TRZEBA TROCHĘ MYSLIĆ, STOSOWAĆ DO RACHUNKÓW TROCHĘ
ALGEBRY I ARYTMETYKI ( NP.WZORÓW SKRÓCONEGO MNOŻENIA , ZAMIANA ZMIENYCH)
I INNE ELEMENTY Z MATEMATYKI, ŻEBY TO CO WYGLĄDA TRUDNE DOPROWADZAĆ DO
CO JEST NAM ZNANE I JEST PROSTE DO ZNALEZENIA.
MAJĄC NADZIEJE ŻE BĘDZIE WAM SŁUŻYŁ TROCHE MOJE SPOTRZEŻENIE NA TEMA
ROZWIĄZYWANIA ZADAŃ.
DO NASTĘPNEGO SPOTKANIA
KOMENTATOR OWMH.
.
1 mar 17:33
Aniusiaaaa: dziękuje
1 mar 17:45
Gustlik: Zgoda, ale wiadomo tutaj, że ujemne rozwiązanie musi odpaść (bo długość boku musi być
dodatnia), wiec nie widzę sensu rozkładania tego na czynniki. Co innego gdybym rozwiązywał
równanie czysto "algebraiczne" nie odnoszące się do długosci boków, wtedy jak najbardziej,
choć ja robię krócej:
y2=49
y=7 v y=−7
Po prostu jak jest potęga parzysta, to muszą być dwa pierwiastki.
1 mar 23:53
komentator OWMH:
Komentarz :
tutaj nie chodzi o rozkadaniu na czynnyki tylko o poprawny rozwiazanie równania
którego jest wynikiem treści naszego zadania owszem oczywiscie jest że długość jest
dodatnią ale zapominać że
√y2nie równa się y.
√y2 = IyI i wracamy znowu do rozwiązaniem równanie z
modułem (wartość bezwzgledna); który jest wiele trudniejsze do zrozumienia dla ucznia;
bo jest pojęcia bardziej bliżej do tego co nam otacza (odlegóści ) i z samego zapisu bez
interpretacji geometryczne; nie ma wartosci dla ucznia, można potraktować jako f−cji.
przepraszam ale nie można lekceważyć to co jest ścisłej określony w matematyce
musi być jednoznaczności określenia danego pojęcia.
przepraszam , sorry
!
komentator OWMH
2 mar 00:28
komentator OWMH:
przepraszam co to jest rozwiazać czysto algebraiczne
?
2 mar 00:29
komentator OWMH: rozwiazuje się równanie doprowadzając do nastepnego r−nia równoważne do poprzedniego
tak tyle razy aż dojdziemy do taki postaci trywialnej ( gdzie ławto określić jego zbiór
rozwiązania)
pamiętamy że dwa równanie są rownoważne kiedy mają ten sam zbiór rozwiązanie.
własnie to jest cała esencja przy rozwiązywaniu równań.
Dobranoc
komentator OWMH
2 mar 00:38