Pole
xxxMimixxx:
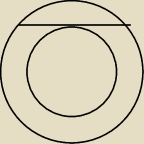
Dane są dwa współśrodkowe okręgi. Cięciwa większego okręgu styczna do mniejszego okręgu ma
długość 10. Oblicz pole pierścienia utworzonego przez te okręgi.
POMOCY
!
28 lut 19:53
xxxMimixxx: 
28 lut 19:58
ICSP: Nie jestem pewien ale chyba 25.
28 lut 20:06
xxxMimixxx: ale jak to wyliczyłeś/aś? Ja potrzebuje też obliczenia
28 lut 20:07
ICSP: Masz chociaż odpowiedzi?
28 lut 20:07
xxxMimixxx: nie nie mam
28 lut 20:08
ICSP: To wolę nie wprowadzać w błąd gdyby moje rozumowanie było błędne.
28 lut 20:10
mikołaj: najwyżej, proszę pomóż mi
28 lut 20:10
Zimny:
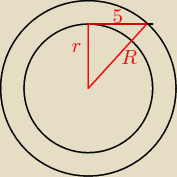
z tw.pit:
R
2=r
2+25
P=πR
2−πr
2
Wstawiamy za R
2
P=πr
2 + 25π − πr
2
P=25π
28 lut 20:12
Emil: można to sprowadzić do skrajnego przypadku, że mniejszy okrąg jest punktem a ta cięciwa
większego to średnica. czyli wtedy pole większego a jednoczesnie pole pierscienia wynosi 25π.
28 lut 20:14
Komar:
To jest trójkąt prostokątny,czyli r
√2=10
r=5
√2
A to 5 i 5 jest tam również dlatego,że tamto to też trójkąt prostokątny,ten specjalny o kątach
90,45 i 45. W nim przeciwprostokątna ma a
√2.
Więc pole tego dużego koła to π R
2 = π (5
√2)
2 = 2*25π = 50 π
Odjąc pole małego,równe πr
2 = π5
2 = 25 π
Pole tego pierścienia kołowego to 50π−25π=25π,czyli dobrze Ci wyszło.
28 lut 20:14
Zimny: Ciekawe rozwiazanie Emil
28 lut 20:15
xxxMimixxx: i to będzie wszystko
A to może wynik wyjść z π
28 lut 20:16
Emil: dzięki
na pitagorasa nawet nie wpadłem
28 lut 20:16
Zimny: Tak , zawsze sie zostawia π , jesli w poleceniu nie ma nic o tym zeby zamienic.
28 lut 20:16
Emil: byłoby niespotykane gdyby wyszło bez π
28 lut 20:17
xxxMimixxx: aha, bo my zawsze to zamienialiśmy...
28 lut 20:22