prawdopodobieństwo w sondażu gorskierr: Według sondażu przeprowadzonego w pewnym miasteczku 13% mieszkańców czyta poezję i nie pali papierosów, 1%nie czyta poezji, zaś pali papierosy, a 79% mieszkańców to osoby, które nie palą papierosów i nie są miłośnikami poezji. Oblicz prawdopodobieństwo tego, że losowo wybrany mieszkaniec: a) czyta poezję lub pali papierosy b) jest palaczem czytającym poezję odpowiedź powinna wynosić a− 0,21 b− 0,07

adrian: A − poezja B − papierosy P(A∩B') = 0,13 = P(A) − P(A∩B) P(A'∩B) = 0,01 = P(B) − P(A∩B) P(A'∩B') = 0,79 = P(AuB) ' −> z prawa de Morgana P(AuB) = 1 − P(AuB)' = 1−0,79=0,21 Ze wzoru mamy: P(AuB) = P(A) + P(B) − P(A∩B) P(A∩B) = P(A) + P(B) − P(AuB) P(A∩B) = 0,13 + P(A∩B) + 0,01 + P(A∩B) − P(AuB) P(A∩B) = 0,21 − 0,13 − 0,01 = 0,07 Podstawiamy: 0,13 + P(A∩B)= P(A) 0,01 + P(A∩B)= P(B)

gorskierr: dziękuję : ))

Basia: A − czyta poezję B − pali P(A∩B') = 0,13 P(A'∩B) = 0,1 P(A'∩B') = 0,79 (a) P(A∪B) = 1 − P[ (A∪B)'] = 1−P(A'∩B') = ............ dokończ (b) P(A∩B) = ? P(A∩B')+P(A'∩B') = P[ (A∩B')∪(A'∩B') ] (bo to są zbiory rozłączne) = P(B') P(B') = 0,13+0,79 = 0,92 P(B) = 0,08 P(A'∩B)+P(A'∩B') = P[(A'∩B)∪(A'∩B')] (jak wyżej) = P(A') P(A') = 0,1+0,79 = 0,8 P(A) = 0,2 P(A∪B) = P(A)+P(B)−P(A∩B) podstaw i wylicz

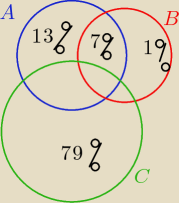
Eta: 13%+1%+79% = 93% 100% −93%= 7% A −− czytają poezję −−− 0,13 B −− palą papierosy −−− 0,01 C −− nie czytają i nie palą −−− 0,79 A∩B −−− czytają poezję i palą papierosy −−− 0,07 a) A U B −−− czytają lub palą −−−− 0,13 + 0,07 + 0,01= 0,21 b) A ∩ B = 0,07 −−− palacze czytający poezję

Eta:

gorskierr: dzięki : ))