proszęę.. piernik: dany jest ostrosłup prawidłowy czworokątny o podstawie ABCD i wierzchołku S. pole trójkąta ACS jest równe 20√2, krawędź boczna jest nachylona do płaszczyzny podstawy pod kątem, którego tangens jest równy ^5√2₄. oblicz objętość ostrosłupa.

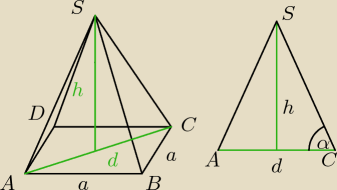
dero2005: z trójkąta po prawej stronie wynika, że :

2h		5√2		5d√2
	= tg α =		→ h =
d		4		8

	d*h
pole tego trójkąta wynosi 20√2 =
	2

d*h = 40√2 wstawiamy h

	5d√2
d*		= 40√2
	8

5d² = 320 d² = 64 z drugiej strony d² = 2a² zatem a = 4√2 mając a i h możemy policzyć objętość ze wzoru V = ¹₃a²*h = do policzenia