| 2√3 | ||
Oblicz sinα *cosα , jeśli cosα + cosβ = | , a α i β to kąty ostre trójkąta | |
| 3 |
| 2√3 | ||
cosα + cosβ = | /2 | |
| 3 |
| 4 | ||
cos2α + 2cosαcosβ + cos2β = | cosβ = sinα | |
| 3 |
| 4 | ||
cos2α + 2cosαsinα + sin2α = | ||
| 3 |
| 4 | ||
1 + 2cosαsinα = | ||
| 3 |
| 1 | ||
2cosαsinα = | ||
| 3 |
| 1 | ||
cosα * sinα = | ||
| 6 |
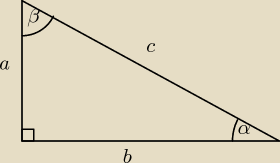
| a | ||
cosβ = | = sinα, czyli: | |
| c |
| 2√3 | ||
cosα + sinα = | /2 | |
| 3 |
| 4 | ||
cos2α + sin2α + 2sinαcosα = | ||
| 3 |
| 4 | ||
1 + 2sinαcosα = | ||
| 3 |
| 1 | ||
2sinαcosα = | ||
| 3 |
| 1 | ||
sinαcosα = | . | |
| 6 |


