Horsemen: W trójkącie boki mają długości 13 cm, 14 cm, 15 cm. Oblicz długość promienia okręgu, którego środek leży na najdłuższym boku i stycznego do pozostałych boków tego trójkąta.

Krecik:

pigor: ..., np. tak : niech r= ? − szukana długość promienia, α − kąt między bokami dł. 13 i 14, to z tw. cosinusów

	132+142−152		132−1*29		140
cosα=		=		=		= 513,
	2*13*14		2*13*14		13*28

czyli sin²α= 1−²⁵₁₆₉ = ¹⁴⁴₁₆₉ ⇒ sinα= ¹²₁₃, stąd, z własności stycznej do okręgu i równości pola danego Δ : ¹₂r*13+¹₂r*14 = ¹₂13*14sinα ⇔ r(13+14) = 13*14*¹²₁₃ ⇔ ⇔ 27r = 12*14 ⇔ 9r = 56 ⇔ r = ⁵⁶₉ = 6 ²₉ cm. ...

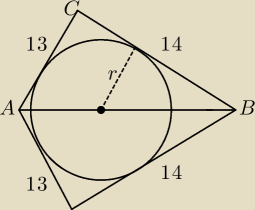
Pustak: Inny sposób: |AB| = 15 Korzystając z wzoru Herona dla trójkąta ABC:

	1
pt =		(13 + 14 + 15} = 21, 21 − 13 = 8, 21 − 14 = 7, 21 − 15 = 6.
	2

Pole trójkąta ABC P_Δ = √21*8*7*6 = 84

	1
Dla czworokąta p =		(2*13 + 2*14) = 27
	2

	168		56
Pole czworokąta P = 2*84 = 168 i P = p*r to 168 = 27*r stąd r =		=
	27		9