Zadanka dla Godzia :))) Gustlik: Fajne zadanka dla Godzia 1. Zbadaj przebieg funkcji

	2x2−5x+2
f(x)=
	3x2−10x+3

2. Wiedząc, ze x₁ i x₂ są pierwiastkami równania kwadratowego

	1
(m2−1)x2−2x+		=0
	4

zbadaj przebieg funkcji f(m)=x₁+x₂ i naszkicuj jej wykres. 3. W pewnym doświadczeniu proton o energii kinetycznej E_k=2 MeV kraży po torze kołowym w płaszczyźnie prostopadłej do linii jednorodnego pola magnetycznego. Jaką energię kinetyczną będzie miał a) deuteron b) cząstka α poruszające się po takim samym torze? Przyjąć m_d≈2m_p oraz m_α≈4m_p, gdzie m_p to masa spoczynkowa protonu. Pozdrawiam

Eta: Gustlik ......zamęczysz Godzia Pozdrawiam obydwu Panów

Gustlik: Może i zamęczę, ale obiecałem Godziowi dzisiaj łamigłówki matematyczne i słowa dotrzymuję. A poza tym Godzio jest dobry z pochodnych, więc dla niego to pikuś i da radę, poza tym i na maturze, a już na pewno na studiach na Politechnice taki trening z matmy i fizy się przyda. Pozdrawiam i Ciebie i Godzia.

Godzio: Witam , już się zabieram

Godzio: Gustlik możesz napisać co ma się zawierać w tym 1 zdaniu ? −monotoniczność −ekstrema −dziedzina −zbiór wartości −punkty przegięcia −wklęsłość −asymptoty Coś jeszcze ?

Gustlik: Ja to robię tak: 1. Dziedzina. 2. Punkty przecięcia z osiami, tj. miejsca zerowe i oś OY. 3. Inne własności funkcji, np. parzystość, okresowość. 4. Granice na krańcach dziedziny, tj. +−∞ oraz w punktach nie należących do dziedziny. 5. Asymptoty. 6. Pochodna. 7. Ekstrema i monotoniczność. 8. II pochodna. 9. Punkty przegięcia i wklęsłość. 10. Tabelka. 11. Wykres. Trochę tego jest, ale zabawa jest przednia. Pozdrawiam.

Godzio: Już wszystko prawie mam prócz wykresu, punktów przegięcia i wklęsłość, i tu właśnie się zatrzymałem otrzymałem przy liczeniu wklęsłości takie coś:

	1
f''(x) > 0 ⇒ (3x3 − 9x + 10)(x − 3)(x −		) > 0 −− możesz powiedzieć czy dotąd jest
	3

dobrze i czy da się wyznaczyć jakoś pierwiastki z tego 3x³ − 9x + 10 ?

Gustlik: Poczekaj chwilę, policze obie pochodne i sprawdzę...

Gustlik:

	90x3−150x+100
Mi druga pochodna wyszła f'(x)=		, ale nie wiem, czy nie ma
	(3x2−10x+3)3)

błędu, bo było trochę liczenia. A jaka Ty masz II pochodną?

Godzio: no mi właśnie wyszło

30x3 − 90x + 100
(3x2 − 10x + 3)3

Gustlik: Poczekaj, sprawdzę jeszcze, bo ktoś z nas ma błąd.

Gustlik: Godzio, znalazłem u siebie drobny błąd rachunkowy, ale wyszło mi teraz w liczniku II pochodnej 30x³−90x²−90x+100, a więc jakby jeden wyraz nie pasował. A jaką masz I pochodną?

Godzio:

	−5x2 + 5
f'(x) =
	(3x2 − 10x + 3)2

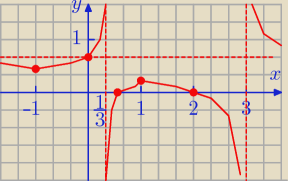
Godzio: Dobra wrzucam odpowiedź bo mi sie jeszcze coś zatnie a nie chce tego stracić wszystkiego

	2x2 − 5x + 2
f(x) =
	3x2 − 10x + 3

	10 + 8		10 − 8		1
3x2 − 10x + 3 ≠ 0 ⇒ Δ = 64, √Δ = 8, x1 =		= 3, x2 =		=
	6		6		3

	1
D = R − {		,3}
	3

Miejsca zerowe:

	5 + 3		5 − 3		1
Δ = 9, √Δ = 3, x1 =		= 2, x2 =		=
	4		4		2

	2
Punkt przecięcia z osią OY:
	3

	1		9
ZW = (−∞,		)∪(		,∞)
	4		16

	(4x − 5)(3x2 − 10x + 3) − (2x2 − 5x + 2)(6x − 10)
f'(x) =		=
	(3x2 − 10x + 3)2

	−5x2 + 5
=
	(3x2 − 10x + 3)2

Funkcja nie jest parzysta, ani nieparzysta, ani okresowa

	1		1
f'(x) > 0 ⇒ −5x2 + 5 > 0 ⇒ −5(x2 − 1) > 0 ⇒ x ∊ (−1,1) ⇒ f ↗ (−1,		), (		,1)
	3		3

f'(x) < 0 ⇒ x ∊ (−∞,−1)∪(1,∞) ⇒ f↘ (−∞,−1), (1,3), (3,∞)

	9		9
Minimum lokalne: f(−1) =		(−1,		)
	16		16

	1		1
Maksimum lokalne: f(1) =		(1,		)
	4		4

	−10x(3x2 − 10x + 3)2 + 2(5x2 − 5)(3x2 − 10x + 3)(6x − 10)
f''(x) =		=
	(3x2 − 10x + 3)4

−10x(3x2 − 10x + 3) + 2(5x2 − 5)(6x − 10)
	=
(3x2 − 10x + 3)3

−30x3 + 100x2 − 30x + 2(30x3 − 50x2 − 30x + 50)
	=
(3x2 − 10x + 3)3

−30x3 + 100x2 − 30x + 60x3 − 100x2 − 60x + 100
(3x2 − 10x + 3)3

	30x3 − 90x + 100
f''(x) =
	(3x2 − 10x + 3)3

f''(x) > 0 ⇔ (30x³ − 90x + 100)(3x² − 10x + 3) > 0 (30x³ − 90x + 100)(3x² − 10x + 3) > 0

	1
(3x3 − 9x + 10)(x − 3)(x −		) > 0 nie mam pojęcia jak wyznaczyć pierwiastki
	3

	2x2 − 5x + 2		2
limx→∞		→		,
	3x2 − 10x + 3		3

	2x2 − 5x + 2		2
limx→−∞		→
	3x2 − 10x + 3		3

	2
asymptota pozioma obustronna: y =
	3

	2x2 − 5x + 2
limx→1/3−		→ +∞
	3x2 − 10x + 3

	2x2 − 5x + 2
limx→1/3+		→ −∞
	3x2 − 10x + 3

	2x2 − 5x + 2
limx→3−		→ −∞
	3x2 − 10x + 3

	2x2 − 5x + 2
limx→3+		→ +∞
	3x2 − 10x + 3

	1
asymptoty pionowe obustronne: x =		i x = 3
	3

	2x2 − 5x + 2   3x2 − 10x + 3
limx→±∞		=
	x

	2x − 5 + 2/x
= limx→±∞		→ 0 − brak asymptoty ukośnej
	3x2 − 10x + 3

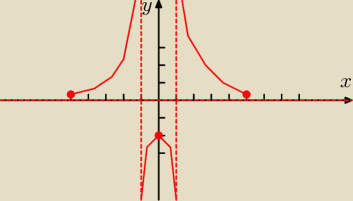
Godzio: Zad. 2

	1
(m2 − 1)x2 − 2x +		= 0
	4

m ≠ 1 i m ≠ −1 Δ ≥ 0 ⇒ 4 − (m² − 1) = −m² + 5 ⇒ m ∊ <−5,5>

	2
f(m) =
	m2 − 1

D = <−5,−1) ∪(−1,1) ∪ (1,5> Miejsc zerowych brak, punkt przecięcia z OY: −2

	−4m
f'(m) =
	(m2 − 1)2

f'(m) > 0 ⇔ m < 0 ⇒ f↗ <−5,−1), (−1,0) f'(m) < 0 ⇔ m > 0 ⇒ f ↘ (0,1), (1,5>

	1		1		1		1
Minimum lokalne: f(−5) =		oraz f(5) =		⇒ (−5,		) (5,		)
	12		12		12		12

	−4(m2 − 1)2 + 4m * 2(m2 − 1) * 2m
f''(m) =		=
	(m2 − 1)4

	−4m2 + 4 + 16m2		12m2 + 4
=		=
	(m2 − 1)3		(m2 − 1)3

f''(m) > 0 ⇔ (12m² + 4)(m² − 1) > 0 ⇒ funkcja jest wypukła dla <−5,−1) (1,5> f''(m) < 0 −− funkcja jest wklęsła (−1,1) Brak punktów przegięcia

	2
limm→±∞		→ 0
	m2 − 1

	2
limm→1−		→ ∞
	m2 − 1

	2
limm→1+		→ −∞
	m2 − 1

	2
limm→−1−		→ ∞
	m2 − 1

	2
limm→−1+		→ − ∞
	m2 − 1

	2   m2 − 1
limm→±∞		→ 0 −− brak ukośnych
	m

asymptota pozioma obustronna: y = 0 asymptoty pionowe obustronne: x = 1 i x = −1 Funkcja jest parzysta

Gustlik: Masz dobrze obliczone, jeszcze raz obliczyłem, wyszło mi tak samo. Wkradł się błąd, ale go znalazłem. Trochę ciężko tu znaleść pierwiastek, bo ani całkowite ani wymierne nie wychodzą.

Godzio: Tego z fizyki nie zrobię, możesz zostawić to bo w piątek mam z tego spr to do tego wrócę jak się nauczę a teraz mi się już nie chce do tego wracać

Godzio: W zad.1 ZW, przydały miały byś domknięte

Godzio: przedziały miały być domknięte *

Gustlik: Masz dobrze oba zadania.

Godzio: ufff to dobrze, trochę mi to zajęło

Gustlik: Mają być domknięte, bo wykres ma wierzchołki, a one muszą należeć do ZW.

Gustlik: Z asymptotami wyczaiłem jedna fajną własność: istnienie asymptoty poziomej w danym przedziale automatycznie wyklucza istnienie asymptoty ukosnej w tym przedziale, a właściwie ukośna będzie poziomą bo wychodzi wtedy a=o, a b jest takie samo jak przy asymptocie poziomej.

Godzio: Zapamiętam

Papi :): Zbadaj m²x +3=9x−m

Eta: Nie wyciągaj starych postów, ......... załóż nowy !

Godzio: Post z moimi męczarniami

Eta:

Trivial: Godzio, co to za męczarnie! O.O

Godzio: Rzemiosło !

Eta: