Ciekawe zadanko dla Godzia :))) Gustlik: W pierwszej urnie znajdują się kartki z napisanymi na nich liczbami:

	7		4		2		4		4
log√327, sin		π, log		(		) (		− podstawa logarytmu), tg		π
	6		9		3		9		3

	π		1		1
a w drugiej z liczbami log9tg		, log		(2√2) (		− podstawa logarytmu),
	6		2		2

	2n2−1
limn→∞
	n−n2

Rzucamy kostką do gry. Jeżeli wypadnie liczba oczek nie większa od 4, to losujemy kartkę z pierwszej urny, w przeciwnym przypadku z drugiej urny. Oblicz prawdopodobieństwo wylosowania kartki z liczbą spełniająca nierówność: x²≤1.

kropek : to zad jest proste trzeba powyliczac co znajduje sie w urnach potem rozwiazac nierownosc i skorzystac z klasycznej def prawdopodobienstwa

Gustlik: Ja wiem, znam to zadanie, bo sam je rozwiązywałem, tylko zadałem je Godziowi, bo chłopak zdaje maturę.rozszerzoną. Ja nie oczekuję pomocy, ale dzięki za podpowiedź. Pozdrawiam

kropek : no spoko to powodzenia

Godzio: Zaraz się w to pobawię ale muszę chwilę odsapnąć bo dopiero wróciłem do domu

Godzio: 1) log_√327 = 6

	7		π		π		1
sin		π = sin(π +		) = −sin		= −
	6		6		6		2

	2		1
log4/9		=
	3		2

	4		π		π
tg		π = tg(π +		) = tg		= √3
	3		3		3

2)

	π		√3		1
log9tg		= log9		⇒ 32x = 3−1/2 ⇒ x = −
	6		3		4

	3
log1/22√2 = −
	2

	2n2 − 1		2 − 1/n2
limn→∞		= limn→∞		→ − 2
	n − n2		1/m − 1

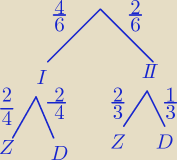
x² ≤ 1 ⇒ x ∊ <−1,1> D − dobre liczby Z − złe liczby

	4		2		2		1		2		1		4
P(D) =		*		+		*		=		+		=
	6		4		6		3		6		9		9

Gustlik: OK, super. Masz tylko mały błąd "w druku" w granicy, bo napisałeś w manowniku 1/m, zamiast 1/n, ale to nie ma wpływu na rozwiązanie. Pozdrawiam

Godzio: Ufff nie byłem do końca pewien rozwiązania

Gustlik: Godzio − zamieściłem Ci jeszcze jedno fajne zadanko, ale chyba nieco prostsze od tego lecz też na poziomie matury rozszerzonej. Wiem, że lubisz matmę, tak jak ja,, dla mnie takie zadanka to rodzaj rozrywli i łamigłówki. Pozdrawiam

Kasia:

	4		2
Może mi ktoś wytłumaczyć czemu przy urnach jest		I		? Proszę o pomoc.
	6		6

Janek191: Liczby nie większe od 4 to 1, 2, 3, 4 − jest ich 4 więc

4		2
	, w przeciwnym przypadku mamy liczby 5 i 6 , czyli
6		6

Kasia: Aha myślałam że mamy wziąć pod uwagę liczby z urny, dziękuję bardzo.