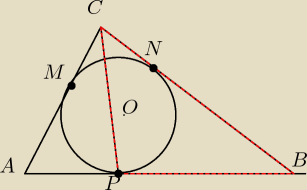
Planimetria - obwód trójkąta, Raff: Proszę o pomoc − planimetria: W trójkąt prostokątny ABC wpisano okrąg. Punkty M, N, P są punktami styczności okręgu odpowiednio z bokami AC, BC oraz AB. Przeciwprostokątna AB ma długość 20 cm, a długości przyprostokątnych pozostają w stosunku |AC| : |BC| = 3 : 4. Oblicz obwód trójkąta PBC.

Renia: Czyli AC=3x BC=4x Z trójkąta Pitagorejskiego AB=5x 5x=20 x=4 P trójkąta=1/2*AC*BC P=0,5*12*16=96 Obw ABC=12x=12*4=48 Pole trójkąta obliczymy jako połowa obwodu razy promień okręgu wpisanego P=0,5*48*r=24r 24r=96 r=4 CM=CN=r=4 AM=AP=AC=r=12−4=8 PB=AB−AP=20−8=12 Kąt ABC=α czyli cos α=BC/AB cosα=16/20=4/5 PC liczysz z twierdzenia cosinusów i już masz obwód

Raff: Wszystko wyszło jak należy, dzięki!