/j^p/ was: Dany jest trójkąt prostokątny ABC o kącie prostym przy wierzchołku C. Poprowadzono w tym trójkącie prostą równoległą do przeciwprostokątnej która przecięła bok AC w punkcie D i bok BC w punkcie E. Oblicz długości przyprostokątnych trójkąta ABC wiedząc, że |DE| =a. |∡ABC| = |∡DAE|=α

was:

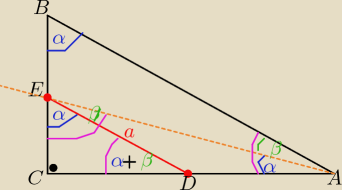
Eta: Zuważ trzy trójkąty prostokątne podobne z cechy ( k,k,k) ΔABC ~ ΔACE ~ ΔDCE z ΔDEC :

	|CE|
		= cosα ... => |CE|= a*cosα
	a

z ΔACE:

	|AC|		cosα
		=ctgα ...... => |AC|=|EC|*ctgα= a*cosα*
	|EC|		sinα

	a*cos2α
zatem: |AC|=
	sinα

z ΔABC:

	|AC|		|AC|		acos2α		cosα
		= tgα ........ => |BC|=		=		*
	|BC|		tgα		sinα		sinα

	acos3α
zatem: |BC|=
	sin2α

fd: dfg