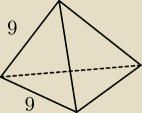
Graniastosłupy Piotrek.: Witam chciałbym aby ktoś rozwiązał mi to zadanie. Pewnie każdy myśli ,że chce gotowca. Tak ,chcę ponieważ kiedy dostał bym 4−5 podciągnął bym swoją średnia z 1.67 na −−−− .Skręciłem rzepkę i teraz to lipa takie zaległości. Więc z góry dziękuję jeżeli ktoś się zlituję i mi pomoże. Na rysunkach przedstawione są ostrosłupy prawidłowe. oblicz pole powierzchni całkowitej i objętość każdego z tych ostrosłupów. Mianowicie chodzi mi o ten : Dziękuję jeszcze raz.

ICSP: Czworościan foremny... Krawędź oznaczamy jako a Dla czworościanu foremnego są następujące wzorki:

	a3√2
v =
	12

P = a²√3

Piotrek.: Przepraszam Cię ale totalnie nie rozumiem co mam z tym zrobić dla tego proszę o pomoc właśnie was... Jeżeli nikt nie pomoże ,rozumiem. To nie forum od tego.

ICSP: Już ci mówię. Czworościan foremny jest to taki ostrosłup który ma wszystkie krawedzie równej długości. Ostrosłup prawidłowy to taki któy w podstawie ma wielokąt foremny Przykłady wielokątów foremnych: trójkąt równoboczny kwadrat sześciokąt foremny

Piotrek.: Hmm a więc tak? Pp=a²√3/4=9√3 Wysokość boku 3²+h²=9² h²=81−9=72 h=√72=6√2 Pb=3*½*6*6√2=54√2 Pc=9√3+54√2 H²+(√3)²=(6√2)² H²=72−3=69 H=√69 V=⅓*Pp*H=⅓*9√3*√69=3√207=9√23

ICSP: Strasznie na około... Skoro czworościan foremny ma wszystkie krawędzie równej długości to wszyskie jego ściany będą miały równe pole(podstawa i ściany boczne) pole jednego trójkąta równobocznego(nie zapominaj o wszystkich krawędziach równej długości) jest równe:

	a2√3
P =		. Czworościan ma cztery śiciany stąd pole czworościanu:
	4

p = U{a²√3{4} * 4 = a²√3. W twoim przypadku a = 9 P = 81√3

Piotrek.: Hmm coś niby zaczynam świtać. Ale przecież nie ma wszystkich obliczeń .

ICSP: nie ma wszystkich obliczeń? Tzn.?

Piotrek.: a2√3 P = . Czworościan ma cztery śiciany stąd pole czworościanu: 4 p = U{a2√3{4} * 4 = a2√3. W twoim przypadku a = 9 P = 81√3 Tylko tyle? i już obliczone? Nie powinno być coś jeszcze? Bo jakoś nie mogę do tego dojść

ICSP: Tylko tyle. Została jeszcze objętość.

ICSP: https://matematykaszkolna.pl/strona/992.html − tutaj masz wyprowadzony wzór na objętosć czworościanu foremnego.

Piotrek.: Hmm zaraz potrenuję jeszcze bo mam taki podobny ostrosłup. Wiem ,że jeszcze objętość hmm. Robiłem już takie 3 ostrosłupy i ten jest jakiś dziwny. I nie wiem co to za p =" U "{a2√3{4} * 4 = a2√3. Co to jest te U. Jestem w gimnazjum i bardziej przydało by mi się to napisać "pogimnazjalsku"

ICSP: to U to jest ułamek używany na tej stronce dla zapisanie dla przykładu:

2
	zapisuję jako U{2}{3 tylko zapominałem tam gdzieś dodać takie nawiasu: ] no i powstało
3

takie cos

Piotrek.: Kurdę pomieszało mi się... wszystko już. Wiem że o dużo proszę ale czy mógłbyś to napisać jeszcze raz ja na prawdę jestem słaby z matematyki i jak chciałbym TYLKO gotowca to by juz mnie tu nie było nie męczył bym sie ja po prostu uczę się z kogoś przykładu a mnie w szkole nie było kupe czasu.

Piotrek.: Proszę ,błagam was. Pomóżcie mi ; /

ICSP: P = a²√3 a = 9 P = 81√3

	a3√2
V =
	12

a = 9

	729√3		243√2
V =		=
	12		4

Proponowałby przepisać jeszcze wyznaczanie tych wzorów ze strony którą wyżej podałem.

Piotrek.: Kurdę dziękuję Ci bardzo.. Lecz i tak mam małe zastrzeżenia babka wie że ja słaby jestem i jak jej to dam w 5 linijkach to nie wiem co to będzie ale i tak dzięki wielkie. Myslałem że będzie tego dużo tak jak ja mam w zeszycie po całą stronę pisania.Oki przepiszę.

Piotrek.: ICSP czy to jest najbardziej jak się da skrócone ? Jak tak to czy da się to bardziej rozpisać?

Piotrek.: Widzę że ICPS już nie ma więc mógłby mi ktoś powiedzieć czy to co jest napisane 3 posty wyżej da się bardziej rozpisać?

ICSP: Tzn chcesz to bardziej rozpisać?

Piotrek.: Tak Dokładnie tak (i po co ja robiłem 2 temat "gafa" )

ICSP: Pola bardzije nie skrócę. Już zaczynam pisać objętość.

Piotrek.: Ok ,dzięki

ICSP:

	1
V =		Pp*h
	3

krawędź oznaczam jako a a = 9

	81√3
PP = a2√3{4} =
	4

	1		81√3		81√3
V =		*		* H =		* H
	3		4		12

h − wysokość trójkąta równobocznego znajdującego się w podstawie.

	a√3		9√3
h =		=
	2		2

	2
Liczę promień okręgu opisanego na tym trójkącie(		h)
	3

2		9√3
	*		= 3√3
3		2

Tworzę trójkąt prostokątny z użyciem wysokości promienia okregu opisanego oraz krawedzi bocznej: (3√3)² + H² = 9² ⇔ H² = 81 − 27 ⇔ H² = 54 ⇔ H = √54 ⇔ H = 3√6

	81√3		81√3		81 * 3 * √12		81 * 3 * √2
V =		* H =		* 3√6 =		=		=
	12		12		12		4

	243√2
	4

Piotrek.: O stary dziękuję Ci na prawdę dobry z Ciebie człowiek.

ICSP: Z tym P_p znowu mi nie wyszło tam powinno byc dzielone przez 4 a nie {4}

Piotrek.: (3√3)2 + H2 = 92 ⇔ H2 = 81 − 27 ⇔ H2 = 54 ⇔ H = √54 ⇔ H = 3√6 Co oznaczają te strzałki ? ze to to to ?

Piotrek.: Wiem tam już jakoś przelazłem

ICSP: To są pierwiastki.

ICSP: a te strzałki oznaczają wtedy i tylko wtedy.

ICSP: Można to też przepisywać pod spodem. Te strzałki wprowadza sie w liceum.

Piotrek.: aha hmm tego jeszcze u mnie nie było da radę to jakoś zastapić?

ICSP: Przepisuj pod spodem.

ICSP: (3√3)² + H² = 81 H² = 81 − 27 H² = 54 H = 3√6

Piotrek.: o dzięki dzięki