przekroje ostrosłupów
ICSP: W ostorsłupie prawidłowym czworokątnym wysokość jest równa 6 i tworzy z krawędzią boczną kąt
45o. Ostrosłup ten przecięto płaszczyzną przechodząca przez przekątną podstawy i nachyloną do
podstawy pod kątem 60o. Oblicz pole otrzymanego przekroju.
Jakieś wskazówki. Wiem że jeden bok tego przekroju będzie miał długość 12. Możliwe że będzie to
przekrój równoramienny ale nie wiem co mi daje tutaj ten kąt 60o.
24 lut 19:15
Eta:
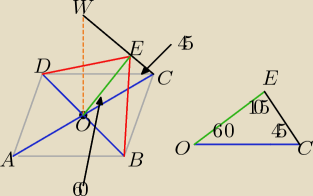
ΔDBE jest równoramienny o podstawie |DB|= 12
|OE|=
h(przekroju)
wyznacz jej długość ze wzoru sinusów
sin105
o= sin(60
o +45
o) =.......
Myślę,że już dalej sobie poradzisz

Sorry za "koślawy" rys.
24 lut 19:50
Eta:
He he

znów chochlik
oczywiście miara kąta E =
75o 
zatem sin75
o= sin( 45
o+ 30
o)
24 lut 19:53
ICSP:
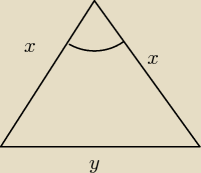
Dziękuję bardzo mam jeszcze jeden problem. Zadanie brzmi:
W ostrosłupie prawidłowym czworokątnym wszystkie krawędzią mają taką samą długość. Oblicz cos
kąta:
zawartego między sąsiednimi ścianami bocznymi. Załączam rysunek jak według mnie będzie wyglądał
trójkąt który będę analizował:
kąta zawarty to kąt szukany
Oczywiście krawędź to a
kąt oznaczam jako γ
| 3 | | 3 | | 3 | | 1 | |
| a2 + |
| a2 − 2 |
| a2 cosγ = |
| a2 |
| 4 | | 4 | | 4 | | 2 | |
| 3 | | 3 | | 1 | |
| a2 − |
| a2cosγ = |
| a2 |
| 2 | | 2 | | 2 | |
| | 1 | |
W odpowiedziach jest − |
| . Nie wiem gdzie błąd robię. |
| | 3 | |
24 lut 19:56
24 lut 20:03
ICSP: Właśnie te odpowiedzi nie dają mi spokoju.
24 lut 20:05
ICSP: Może sprawdź moje rozumowanie. Pewnie gdzieś błąd walnąłem.
24 lut 20:09
Eta:
mój błąd , wynik jest
−13
zaraz Ci narysuję

24 lut 20:33
Eta:
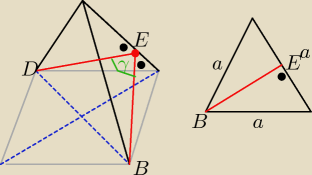
kąt dwuścienny < DEB

z tw. cosinusów
| | h2+h2 − d2 | |
cosγ= |
| =.......
|
| | 2h*h | |
teraz będzie ok

24 lut 20:46
ICSP: Nigdy bym na cos takiego nie wpadł. Bardzo dziękuję jeszcze raz

24 lut 20:48
ICSP: Eta a takie coś:
Krawędź boczna ostrosłupa prawidłowego trójkątnego ma długość 26cm a pole podstawy jest równe
100√3. Ostrosłup ten przecięto płaszczyzną przechodzącą przez środki dwóch krawędzi podstawy
oraz jego wierzchołek. Wykaż że pole otrzymanego przekroju jest większe od 115cm2
Myślę że ten trójkąt będzie trójkątem równoramiennym o ramionach jako wysokości trójkątów
bocznych. Nie wiem tylko jak obliczyć wysokość tego przekroju.
24 lut 20:56
ICSP:
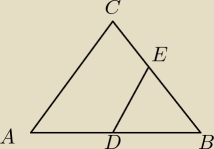
|AB| = 10
trójkąty sa podobne w takim razie DE = 5?
24 lut 22:11
ICSP: |AB| = 20 przecież.
|DE| = 10. wtedy wysokosc przekorju równa sie 5
√11
| | 1 | |
p przekroju = |
| * 10 * 5 √11 25 √11 < 115  . Nadal coś źle. |
| | 2 | |
24 lut 22:16
ICSP: Wyszło

.
24 lut 22:18
Eta:
|AB|=
20 
24 lut 22:27
ICSP: Już zauważyłem

Jeszcze raz dziękuję ci za pomoc

24 lut 22:28
ICSP: Przepraszam. Dziękuję Ci
24 lut 22:28
Eta:
h(przekroju):
h2= 262−(5√3)2
24 lut 22:29
ICSP: mi h wyszło √551
24 lut 22:31
Eta:
sorry to co napisałam ostatnio jest oczywiscie źle

24 lut 22:33
ICSP: Chcesz mnie po prostu zmylić

24 lut 22:35
Eta:
1
o wyznacz dł H −− ostrosłupa
2
o z tw. Pitagorasa w trójkacie prostokatnym H, h, i ten mały odcinek:
| | 2 | |
który ma długość: |
| hp − h trójkąta o boku dł. 10
|
| | 3 | |
teraz powinno być ok

Będę za chwilę, bo muszę coś zjeść

24 lut 22:38
Eta:
Nie "zmylam", bo ten trójkąt który wskazałam wcześniej nie jest prostokątny !
24 lut 22:40
ICSP: Ja to zrobiłem tak:
Najpierw krawędź podstawy wyznaczyłem : 20
Później wyznaczyłem wysokość ściany bocznej − 24
wysokość ściany bocznej jest również ramieniem tego przekroju
Przekrój jest trójkątem równoramiennym
Z podobieństwa trójkątów w podstawie wyliczyłem długość podstawy tego przekroju − 10
twierdzenie pitagorasa i liczę wysokosc przekroju −
√551
| | 1 | |
P = |
| * 10 * √551 = 5√551 ≈ 117,36694. > 115 |
| | 2 | |
Można tak zrobić czy gdzieś jest błąd?
24 lut 22:42
Eta:
Wszystko przez to,że Bozia zapomniał mi dać wyobraźni przestrzennej

24 lut 22:43
Eta:
No i gra

24 lut 22:44
ICSP: Bozia zapomniała dać wyobraźni? Hahaha dobre

Ja tu żadnego zadania nie mogę zrobić a ty ze
swoim brakiem wyobraźni wszystkie robisz

24 lut 22:48
 ΔDBE jest równoramienny o podstawie |DB|= 12
|OE|= h(przekroju)
wyznacz jej długość ze wzoru sinusów
ΔDBE jest równoramienny o podstawie |DB|= 12
|OE|= h(przekroju)
wyznacz jej długość ze wzoru sinusów
 Sorry za "koślawy" rys.
Sorry za "koślawy" rys.
 znów chochlik
oczywiście miara kąta E = 75o
znów chochlik
oczywiście miara kąta E = 75o  zatem sin75o= sin( 45o+ 30o)
zatem sin75o= sin( 45o+ 30o)
 Dziękuję bardzo mam jeszcze jeden problem. Zadanie brzmi:
W ostrosłupie prawidłowym czworokątnym wszystkie krawędzią mają taką samą długość. Oblicz cos
kąta:
zawartego między sąsiednimi ścianami bocznymi. Załączam rysunek jak według mnie będzie wyglądał
trójkąt który będę analizował:
Dziękuję bardzo mam jeszcze jeden problem. Zadanie brzmi:
W ostrosłupie prawidłowym czworokątnym wszystkie krawędzią mają taką samą długość. Oblicz cos
kąta:
zawartego między sąsiednimi ścianami bocznymi. Załączam rysunek jak według mnie będzie wyglądał
trójkąt który będę analizował:

 kąt dwuścienny < DEB
kąt dwuścienny < DEB  z tw. cosinusów
z tw. cosinusów


 |AB| = 10
|AB| = 10
 . Nadal coś źle.
. Nadal coś źle. .
.

 Jeszcze raz dziękuję ci za pomoc
Jeszcze raz dziękuję ci za pomoc


 Będę za chwilę, bo muszę coś zjeść
Będę za chwilę, bo muszę coś zjeść 


 Ja tu żadnego zadania nie mogę zrobić a ty ze
swoim brakiem wyobraźni wszystkie robisz
Ja tu żadnego zadania nie mogę zrobić a ty ze
swoim brakiem wyobraźni wszystkie robisz