Podaj zbiór wartości parametru m, tak aby to równanie miało dwa pierwiastki. Kolin: −x³+2x²−x+2=m²

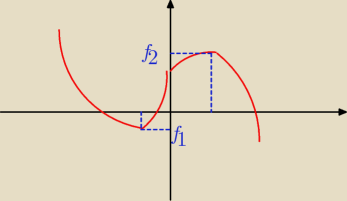
Basia: wykres tej funkcji wygląda mniej więcej tak jak na rysunku f(x) = −x³+2x²−x+2 f'(x) = −3x²+4x−1 Δ=16+12 = 28 = 4*7 √Δ = 2√7

	−4−2√7		2+√7
x1 =		=
	−6		3

	−4+2√7		2−√7
x2 =		=
	−6		3

	2−√7
x∊(−∞,		) ⇒ f'(x)<0 ⇒ f. maleje
	3

	2−√7		2+√7
x∊(		,		) ⇒ f'(x)>0 ⇒ f.rośnie
	3		3

	2+√7
x∊(		,+∞) ⇒ f'(x)<0 ⇒ f. maleje
	3

	2−√7
xmin =
	3

	(2−√7)3		2(2−√7)2		2−√7
f1=fmin =		+		−		+2
	27		9		3

trzeba to niestety policzyć i stwierdzić czy jest ujemne czy dodatnie x_max = U{2+√7{3}

	(2+√7)3		2(2+√7)2		2+√7
f2=fmax =		+		−		+2
	27		9		3

to też do zbioru rozwiązań należą te liczby m, dla których m² = f_min lub m²=f_max

anmario: Aby równanie: −x³+2x²−x+2=m² miało dwa pierwiastki jeden z nich musi być podwójny. W związku z tym, zakładając, że tymi pierwiastkami są liczby a i b równanie to da się zapisać w postaci: −(x−a)²(x−b)=0 Po wykonaniu obliczeń, czyli podniesieniu x−a do kwadratu i wymnożeniu tego co wyjdzie przez x−b dostaniesz: −x³+x²(2a+b)−x(a²+2ab)+a²b=0 Teraz porównujesz to ze swoim równaniem przy czym m² przenosisz na lewą stronę: −x³+2x²−x+2−m² =0 Aby one były takie same współczynniki przy odpowiednich potęgach x muszą być w obydwu równaniach takie same, więc: 2a+b=2 a²+2ab=1 a²b=2−m² Masz układ trzech równań z trzema niewiadomymi. Z pierwszego wyznasz b b=2−2a I podstawiasz to za b w dwóch pozostałych. Dostaniesz układ dwóch równań: 3a²−4a+1=0 −2a³+2a²=2−m² Pierwsze to zwykłe równanie kwadratowe a₁=1 i a₂=3 Tak wyliczone wartości a wstawiasz do drugiego równania i obliczasz m.