Wykaż, że. . . . <3 Ukasz: Wykaż, ze sin15° = √6 − √2 / 4 . PS. Jak tutaj się robi kreskę ułamkową?

AS: Skorzystaj z tożsamości

	1 − cosα
sin(α/2) = √
	2

ICSP: To wszystko jest pod pierwiastkiem.

AS: tak

Eta: sin15^o= sin( 60^o −45^o) korzystamy ze wzoru sin( α−β) = sinα*cosβ− cosα*sinβ sin15^o= sin60^o*cos45^o − cos60^o*sin45⁼ ............ dokończ

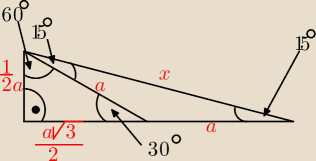
Aerodynamiczny: Witam, a nie da się tego uzasadnić jakoś geometrycznie? Próbowałem to zrobić, zamieszczę rysunek jak to próbowałem zrobić. no i dalej próbowałem obliczyć X z pitagorasa...

	a√3		1
x2=(		+ a)2 + (		a)2
	2		2

	3		1
x2=		a2 + a2√3+ a2 +		a2
	4		4

x²=2a² + a²√3 x²= a²(2+√3) x=a√2+√3 no i pojawia się problem bo jak wyliczam sin15 to nie ma szans żeby wyszło tak jak powinno być. Wydaje mi się że wszystko tu jest dobrze, a może nie Wie ktoś jak to ogarnąć?

PW: A może dobrze policzyłeś, tylko ta liczba występuje pod innym nazwiskiem (wyszła za mąż i teraz się inaczej nazywa)? Spróbuj swój wynik podnieść do kwadratu, i ten ich też.

Aerodynamiczny: sprawdzałem na kalkulatorze i te wartości znacznie się różnią więc coś jest na pewno źle.

	√2 − √3
według mojego rysunku po pewnych obliczeniach wyszło że sin15=
	2

więc jest źle

Aerodynamiczny: jednak te wartości są równe, źle coś policzyłem za pierwszym razem spróbuję z tą potęgą.

PW: Według twoich obliczeń

	2−√3
(sin15°)2 =
	4

Według nich

	√6−√2		6−2√12+2		8−4√3		2−√3
(sin15°)2 = (		)2 =		=		=		.
	4		16		16		4

Mówiłem, że wyszła za mąż? To jest ta sama liczba, oni zapisują tak, żeby nie było pierwiastka pod pierwiastkiem.