witam czy umiał by to ktoś zrobić bym był bardzo wdzięczny ? Wojtek: zad1 Dany jest zbiór oraz zdarzenia , . Wyznacz: , wiedząc, że np. A' jest uzupełnieniem zbioru A do (przykładowo: jeśli A= {a,b,c,d}, ={a,b,c,d,e,f,g}, to A' = {e,f,g}). Oblicz prawdopodobieństwa . zad2 Fabryka kupuje 40% potrzebnych części od producenta A, 35% od producenta B i 25% od producenta C. Wady ma 1% części dostarczonych przez firmę A, 2% − dostarczonych przez producenta B i 4% − dostarczonych przez producenta C. Oblicz prawdopodobieństwo, że wybrana losowo część jest bez wad.

Wojtek: czy umie to ktoś zrobić ?

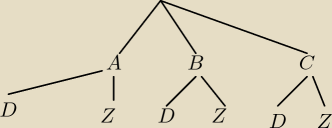
patryk: Zad2 I poziom producent A = 2/5 producent B = 7/20 producent C = 1/4 II poziom producent A − dobre − 99/100 złe − 1/100 producent B − dobre − 98/100 złe − 2/100 producent C − dobre − 96/100 złe − 4/100 Teraz sumujemy dobre z każdej gałęzi

	2		99		7		98		1		96
P(D) =		*		+		*		+		*
	5		100		20		100		4		100

	99		343		979
P(D) =		+		+ U{6}{25) =
	250		1000		1000

patryk: Zadania 1 nie rozumiem o co chodzi, ale może o to, że P(A') = 1 − P(A)

Wojtek: patryk wielki dzięki za to 2 zadanie