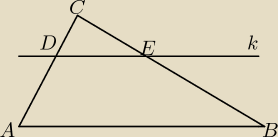
Chyba twierdzenie Tallesa JackBauer: Prosta k równoległa do boku AB trójkąta ABC przecina boki AC oraz BC odpowiednio w punktach D i E. Wiadomo, że pole trójkąta DEC wynosi 4cm², zaś pole trapezu ABED jest równe 8cm². Wykaż,

	|AD|
że		= √3 − 1
	|DC|

Proszę o jakiś pomysł. Na pewno trzeba wykorzystać twierdzenie Tallesa, ale nie wiem w jaki sposób.

JackBauer: Dane: P_DEC = 4 cm² P_ABED = 8cm² Szukane:

	AD
udowodnij, że		= √3 − 1
	DC

JackBauer: Podbijam, proszę o pomoc

JackBauer: nikt mi nie pomoze...?:(

JackBauer: proszę o podpowiedź. mam to na jutro i nie wiem jak kontynuować... Robimy teraz zadania całościowe i nie pamiętam już jak to obliczać.

Bogdan: P₁ = 8, P₂ = 4, |AD| = x, |CD| = y

P1 + P2		x + y		x		x
	= k2 ⇒		= k ⇒		+ 1 = k ⇒		= k − 1
P2		y		y		y

ICSP:

	12
ΔABC ∼ Δ DEC w skali k2 =		⇔ k = √3
	4

|AC|
	= √3 ⇔ |AC| = √3|DC|
|DC|

|AC| = |AD| + |DC| ⇔ √3|DC| − |DC| = |AD| ⇔ |AD| = |DC|(√3 − 1)

|AD|		|DC|(√3 − 1)
	=		= √3 − 1
|DC|		|DC|

JackBauer: w skali k² − mogę wiedzieć skąd to k² się wzięło i co oznacza?

Gustlik: JackBauer, obowiązuje zasada: wzory na pola figur mają strukturę typu P=ax² albo P=axy, gdzie a − stała, x i y − długości odcinków danej figury, np. boków, przekątnych, wysokości itp. Jezęli figurę np. powiększymy albo pomniejszymy k razy, to każdy odcinek zawarty w tej figurze również powiększy się (lub pomniejszy) proporcjonalnie − czyli k razy, a więc wzór na pole przyjmie postać P₂=a(kx)²=ak²x²=k²ax²=k^P lub P₂=a*kx*ky=k²axy=k^axy, bo za x trzeba będzie podstawić kx, a za y ky, jak widac więc P₂=k²*P, zatem stosunek pól figur podobnych wynosi k², k oznacza skalę podobieństwa, czyli inaczej "powiększenie". Można to wytłumaczyć na zasadzie dzialania przyrządów optycznych: zauważ, że jeżeli oglądasz jakiś przedmiot przez przyrząd optyczny (lupę, lornetke itp.) to otrzymany obraz jest figurą podobną do "oryginału", tylko powiekszoną w pewnej skali, w tym przypadku skalą podobieństwa będzie powiększenie przyrządu optycznego. Pozdrawiam

JackBauer: Ogromne dzięki za szczegółową odpowiedź, świetnie to wytłumaczone. Dzięki