dawdawdawd qwerr: Rozwiąż nierówność [2x−3]>1 [a]= oznacza największą liczbę całkowitą nie większą niż a.

awdawda:

awdawda:

awdawda: nikt nie może mi pomóc?

awdawda:

Mila: 2x−3>1 lub 2x−3<−1 2x>4 2x<3 x>2 x<1.5 x∊(−∞,1,5) lub(2,∞)

Godzio: Mila to nie jest wartość bezwzględna

Godzio: [2x − 3] > 1 2x − 3 > 1 ⇒ x > 2 I tyle

Godzio: właściwie x ≥ 3 bo dla (2,3) mamy 1

Mila: ten warunek na |a|,nie wiem

Godzio: Dobra jednak stwierdzam że tutaj musi być x ≥ 2,5 bo od tego momentu zaczyna się wartość 2

Mila:

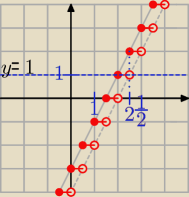
Bogdan: Podaję sposób rozwiązywania równania [f(x)] = b Należy rozwiązać układ: (1) { y = b (2) { y ≤ f(x) ⇒ b ≤ f(x) (3) { y > f(x) − 1 b > f(x) − 1 Np.: [2x − 3] = 1, b = 1 y = 1 i y ≤ 2x − 3 i y > 2x − 4 (można wykonać rysunek z układem współrzędnych)

	1		1
1 ≤ 2x − 3 i 1 > 2x − 4 ⇒ x ≥ 2 i x < 2		⇒ x∊<2, 2		)
	2		2

	1
Jeśli jest: [2x − 3] > 1 ⇒ x ≥ 2
	2

qwerr: a mógłbyś to jakoś jaśniej wytłumaczyć ? y=1 bo b=1 ? y≤2x=3 i y>2x−4 (skad to się wzieło)

qwerr:

kropek : odpowiedz bedzie dla x≥3

Bogdan:

	1
kropek − podałem odpowiedź, x ≥ 2		, a Ty teraz podajesz inną odpowiedź, czyli
	2

nie zgadzasz się z moją odpowiedzią. Jeśli tak, to wskaż w moim rozwiązaniu błąd i uzasadnij poprawność swojego rozwiązania, a jeśli tego nie potrafisz, to nie podawaj innej odpowiedzi, bo robisz zamieszanie.

kropek : przepraszam to ja zamuliłem bo pomyslałem ze x sa wartosciami całkowitymi sorki

karolajn: a mógłbyś to jakoś jaśniej wytłumaczyć ? y=1 bo b=1 ? y≤2x=3 i y>2x−4 (skad to się wzieło)

kropek : Należy rozwiązać układ: (1) { y = b (2) { y ≤ f(x) ⇒ b ≤ f(x) (3) { y > f(x) − 1 b > f(x) − 1 przeanalizuj co tu napisał

kropek : [2x−3] to jest Twoj y czyli lewa str 1 to jest b czyli prawa strona

karolajn: A mógłbyś mi to jakoś rozpisać krok po kroku ?

Basia: KOCHANI na samym początku autor wyraźnie napisał, że chodzi o entier, a nie o wartość bezwzględną (MIla), ani nie o żadne inne cudo Godziu tak najlepiej to robić, żeby nie namieszać entier jest liczbą całkowitą liczba całkowita > k ⇔ jest ≥ k+1 [2x−3] > 1 ⇔ [2x−3] ≥ 2 ⇔ 2x−3 ≥ 2 ⇔ 2x ≥ 5 ⇔ x≥ 2,5

Basia: oczywiście dla k∊C

karolajn: I wystarczy, że przy takim zadaniu na klasówce napisze do co napisała Basia?

Basia: wystarczy a jak miałbyś [2x−3] > ³₂ robisz tam samo [2x−3] > ³₂ ⇔ [2x−3] ≥2 [2x−3] > 5,1 ⇔ [2x−3] ≥ 6 ale [2x−3] < 1 ⇔ 2x−3 < 1 [2x−3] < 1,1 ⇔ [2x−3]≤ 1 ⇔ 2x−3≤1 itd.

bolo: Już myślałem, że to rozuemiem. Napisz mi dokładnie jak to liczysz, może się połapie.

cla: Pomóżcie mi, bo zaraz dostane szału ;< mam taka se o prosta nierownosc : (3/x)<2+x rozwiazuje to juz nty raz i dupa z tego wychodzi ;< nie zgadza mi sie z tym co wypluwa mi wolfram