Matura Robi: Mam dwa zadanka z matury rozszerzonej − proszę o wskazówki: 1. Rozwiąż nierówność:

1		1		1		1		1
	+		+		+		+		<0
x(x+1)		(x+1)(x+2)		(x+2)(x+3)		(x+3)(x+4)		(x+4)(x+5)

Czy jest jekiś szybszy sposób niż sprowadzanie do wspólnego mianownika? Bo wychodzą poczwórne nawiasy do wymnażania, jeżeli będe chciał zrobić w standardowy sposób. 2. Jedna z podstaw trapezu wpisanego w okrąg jest średnica okręgu. Stosunek obwodu trapezu do sumy długości jego podstaw jest równy 3:2. Oblicz cosinus kąta ostrego przy podstawie trapezu.

	x
Tu założyłem sobie, że obw=3x, a+b=2x, doszedlem do tego, że cosα=		i nie wiem, co mam
	2a

zrobić z tym a, bo trzeba byłoby policzyć to na x−ach i skrócić i nie mogę dojść. Z góry wielkie dzięki.

reg:

	1		1		1
Wskazówka:		=		−
	n(n + 1)		n		n + 1

Basia: ad.1

1		1		1
	=		−
x(x+1)		x		x+1

1		1		1
	=		−
(x+1)(x+2)		x+1		x+2

itd.

Robi: Dzięki Proszę jeszcze o wskazówkę do drugiego zadanka.

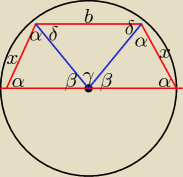
Basia: β=180−2α γ=180−2β=180−2(180−2α) = 4α−180

	180−γ		180−4α+180
δ=		=		= 180−2α
	2		2

a=2r x² = r²+r²−2r*r*cosβ = 2r²−2r²cos(180−2α) = 2r²−2r²*(−cos2α) = 2r²(1+cos2α) = 2r²(1+2cos²α−1) = 4r²cos²α x = 2rcosα b² = r²+r²−2r*r*cosγ = 2r²−2r²*cos(4α−180) = 2r²−2r²*cos(−(180−4α)) = 2r²−2r²*cos(180−4α) = 2r²−2r²*(−cos4α) = 2r²+2r²*cos4α = 2r²(1+cos4α) = 2r²(1+2cos²2α−1) = 4r²cos²2α b = 2rcos2α Ob = a+b+2x

a+b+2x		3
	=
a+b		2

2(a+b+2x)=3(a+b) 2a+2b+4x = 3a+3b 4x = a+b 8rcosα=2r+b 8rcosα=2r+2rcos2α /:2r 4cosα=1+cos2α 4cosα=1+2cos²α−1 4cosα=2cos²α to już da się bez problemu rozwiązać, ale myślę, że powinien być prostszy sposób

Basia: poza tym pomyliłam się gdzieś w rachunkach, bo to równanie nie ma rozwiązania 2cos²α−4cosα=0 2cosα(cosα−2)=0 ⇔ cosα=0 ⇔ α=90 a to jest niemożliwe

Robi: Dzięki

Trivial: (1) a + b + 2c = 3x (2) a + b = 2x → a = 2x − b cosα = ?

	b−a
L =
	2

	c		L		b−a
cosα =		=		=
	b		c		2c

2c² = b(b−a) 2c² = b(b− 2x+b) 2c² = 2b² − 2xb /:2 (3) b² − xb − c² = 0 Trzeba teraz uzależnić x od c. Od równania (1) odejmujemy (2): 2c = x Wstawiamy z powrotem do równania (3): b² − 2cb − c² = 0 Δ_b = 4c² + 4c² √Δ_b = 2√2c

	2c+2√2c
b =		= c(1+√2) // drugie rozwiązanie odpada, bo < 0.
	2

	c		c
cosα =		=		= √2−1.
	b		c(1+√2)

Ciekawe, czy da się jakoś prościej.

Trivial: Masz może do tego odpowiedź?

Basia: w moim rozwiązaniu błąd jest tutaj: b = 2rcos2α lub b = −2rcos2α (bo cos2α może być ujemny) ponieważ b = 2rcos2α doprowadziło do sprzeczności musi być b = −2rcos2α co daje 8rcosα=2r−2rcos2α /:2r 4cosα=1−cos2α 4cosα=1−(2cos²α−1) 4cosα= 1−2cos²α+1 2cos²α+4cosα−2=0 /:2 cos²α+2cosα−1=0 Δ=4+4 = 8 √Δ = 2√2

	−2−2√2
cosα=		= −1−√2 < 0 odpada
	2

	−2+2√2
cosα=		= √2−1
	2

czyli tak samo jak policzył Trivial

Robi: Nie mam, ale serdeczne dzięki. Pozdrawiam

Robi: Dzięki Wam wszystkim