Prawdopodobieństwo
Matt: Wiadomo, że P(A') = 0,7 ; P(A U B) = 0,6 ; P(A' U B') = 0,9 . Oblicz P(B \ A)
Zupełnie nie wiem co zrobić, jedyne co wymodziłem, to P(A) = 0,3 oraz zależność P(A U B) − P (A
∩ B) = P (A \ B)
22 lut 22:20
Kyd: Polecam dogłębne zapoznanie się z tym :
AuB=Au(B\A)
AuB=Bu(A\B)
B=(B−A)u(A∩B)
a=(a−B)u(A∩B)
(A'uB')=(A∩B)'
(A'∩B')=(AuB)'
P(A)=P(A∩B)+P(A−B)
P(∅)=0
P(AuB)=P(A)+P(B)−P(A∩B)
Masz chyba wszystko co Ci potrzeba, a nawet więcej
22 lut 22:24
Matt: Ok, zaraz popróbuję, jak coś będę krzyczał
22 lut 22:25
Kyd: Wszędzie miało być duże 'A' i duże 'B'
22 lut 22:27
Matt: Eh no nie wiem od czego zacząć, potrzebuję P(B) ale żeby to wyliczyć, znowu potrzeba P(A∩B)..
Można tu robić układy równań?
22 lut 22:33
Anek:
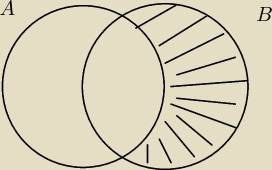
Czyż nie taki będzie rysunek ?
22 lut 22:36
Matt: Tak, mam taki rysunek w notatniku, tylko dalej zaćmienie
Czuję się jak idiota.
22 lut 22:37