Okrąg i koło Dawid: zad.1 Dwa okręgi są styczne zewnętrznie.Odległość między ich środkami wynosi 12cm.Wyznacz długość promieni tych okręgów wiedząc,że jeden z nich jest trzy razy dłuższy od drugiego. zad.2 Dwa okręgi są styczne wewnętrznie.Odległość między ich środkami wynosi 3cm.Wyznacz długość promieni tych okręgow,wiedząc że: a)jeden promień jest dwa razy krótszy od drugiego b)suma długości ich promieni jest równa 17

patryk: 1) 3x + x = 12 ⇒ 4x = 12 ⇒ x = 3. Odpowiedz: Promienie to 3 cm oraz 9 cm.

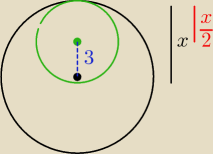
patryk: a) x − promień większego okręgu x/2 − promień mniejszego okręgu

	x		x
x −		= 3 ⇒		= 3 ⇒ x = 6
	2		2

Odpowiedz: Dłuższy promień ma 6 cm a krótszy 3 cm. b) układ równań x − promień większego okręgu y − promień mniejszego okręgu x − y = 3 x + y = 17

Dawid: ⇒ co to oznacza ?

patryk: że drugie równanie wynika z tego pierwszego, trzecie z drugiego itd.

Dawid: a może ktoś mi rozwiązać ten układ równań w punkcie b,bo jakiś dziwny jest

Dawid: a czemu w 1 zadaniu wyszło 9 ?

patryk: Chyba prostszego układu już nie może być... x − y = 3 ⇒ x = 3 +y 3 + y + y = 17 2y = 14 y = 7 x = 7 + 3 = 10 Odpowiedź: większy promień ma 10 cm a krótszy 7 cm.

patryk: no bo większy promień ma jest 3 razy większy, czyli 3x. Skoro x z równania wyszedł 3, no to dłuższy mam 3*3 cm = 9 cm.

patison: Bardzo prosze o pomoc! funkcja f okreslona wzorem f(x)=|x+6|−2|x|+|x+3| ,x∊(−6,0) a)zapisz ta funkcje bez uzycia symbolu wart.bezwzgl. b)narysuj wykrej tej funkcji c)podaj wzor wartosci funkcji f

Dawid: dzięki bardzo

patryk: a) x ∊ (−6; −3) f(x) = x + 6 +2x − x − 3 = 2x +3 x∊ <−3;0) f(x) = x + 6 + 2x + x + 3 = 4x + 9 Odpowiedź:

	⎧	f{x} = 2x +3, x ∊ (−6;3)
f(x) = |x+6| − 2|x| + |x+3|, x ∊ (−6;0) ⇔	⎩	f(x) = 4x+9, x∊<−3;0)

Nie chce mi się rysować, za dużo roboty z tym. Mając już rozbite bez wartości bezwzględnych powinieneś sam narysować.