Pytanie Godzio: Bogdan, co do tego zadania z trapezami, napiszesz mi tu tą podpowiedź czy przez maila ? Chyba już dość dużo h wysiedziałem nad nim i nic prostego nie znalazłem ...

Bogdan: Przed podaniem przez mnie rozwiązania zastanów się, czy trójkąt jest trapezem.

Godzio: Pytanie jest zapewne podchwytliwe, trójkąt nie jest trapezem, ale może chodzi o przedłużenie ramion trapezu do punktu przecięcia ? Jeśli tak to to już też próbowałem

Bogdan: Nie ma nic podchwytliwego w moim pytaniu. Sugeruję, aby spojrzeć na problem w nietypowy sposób i zobaczyć to, co jest poza standardem, co może nawet kłócić się ze zdrowym rozsądkiem i naszą wiedzą. Rozważ trapez, którego górna podstawa jest tylko jednym punktem i ma długość zero. Czy taka figura straciła cechy trapezu?, czym są przekątne w takim trapezie?, jakim wzorem wyraża się pole powierzchni?

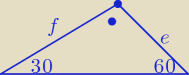
Godzio: W takim przypadku przekątne stają się ramionami f² − e² = 20

	f
tg60 =
	e

f = √3e e² = 10 ⇒ e = √10 f = √30

	ef		√300
P =		=		= 5√3
	2		2

Rzeczywiście dosyć nietypowe, ale czy na takie uproszczenie można sobie pozwolić?

Bogdan: To nie jest uproszczenie. Spróbuj zbadać trapez, którego suma miar kątów ostrych przy podstawie jest równa 90^o, określ cechy takiego trapezu. Czy zmieni się pole powierzchni, jeśli górna podstawa trapezu przyjmie długość zero?

Godzio:

	x
tgα =
	h

x = tgα * h

	y
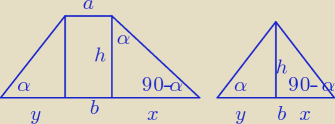
ctgα =
	h

y = h * ctgα b = a + x + y a = b − x − y

	a + b		2b − h(tgα + ctgα)		h2(tgα + ctgα)
P =		* h =		* h = bh −
	2		2		2

	h2(tgα + ctgα)		h2(tgα + ctgα)
bh = 2 *		⇒ P =
	2		2

	hy		hx		h2(ctgα + tgα)
P =		+		=
	2		2		2

Czyli wychodzi że pole zależy tylko i wyłącznie od wysokości, ciekawe. Raczej bym na to nie wpadł, nie jestem jeszcze tak obyty z matematyką żeby niektóre jej elementy widzieć w trochę inny sposób ...

Bogdan: No właśnie Broń się przed schematami myślowymi, które niestety wbijają nam do głów w szkole. Warto spojrzeć czasami na zadanie zapominając wszystkie poznane szablony i wzory i wtedy rozpocząć poszukiwanie rozwiązania. Obserwując Twoje tutaj Godzio zaangażowanie i już posiadane umiejętności wierzę, że dokonasz wielu matematycznych odkryć, czego Ci serdecznie życzę

Godzio: Starałem się spojrzeć na to zadanie jakoś inaczej, poprzestawiać coś w tym trapezie, ale nic nie chciało ciekawego wyjść. Dziękuję za wiarę we mnie, na pewno będę się starał