| 1+√7 | ||
x∊( | ;2) | |
| 2 |
 Najpierw trzeba określić dziedzinę nierówności i przyjąć założenia.
Założenie: 4 − x2 ≥ 0 ⇒ x2 − 4 ≤ 0 ⇒ (x − 2)(x + 2) ≤ 0 ⇒ D: x∊<−2, 2>.
x − √4 − x2 > 1 ⇒ x − 1 > √4 − x2
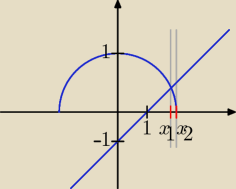
Po lewej stronie nierówności jest linia wzór prostej y = x − 1, po prawej wzór półokręgu
y = √4 − x2 o środku w punkcie O(0, 0) i promieniu r = 2.
......................................................................................
Okrąg o środku O(0, 0) i promieniu r = 2:
x2 + y2 = 4 ⇒ y = √4 − x2 lub y = −√4 − x2
W tym zadaniu występuje y = √4 − x2.
......................................................................................
Widać na rysunku, że linia prosta jest nad półokręgiem w przedziale (x1, x2).
Teraz możemy podnieść obustronnie do kwadratu nierówność x − 1 > √4 − x2
i rozwiązać ją, po uwzględnieniu dziedziny i sytuacji opisanej rysunkiem otrzymamy
odpowiedź podaną przez Marzenę i Tamarę.
Najpierw trzeba określić dziedzinę nierówności i przyjąć założenia.
Założenie: 4 − x2 ≥ 0 ⇒ x2 − 4 ≤ 0 ⇒ (x − 2)(x + 2) ≤ 0 ⇒ D: x∊<−2, 2>.
x − √4 − x2 > 1 ⇒ x − 1 > √4 − x2
Po lewej stronie nierówności jest linia wzór prostej y = x − 1, po prawej wzór półokręgu
y = √4 − x2 o środku w punkcie O(0, 0) i promieniu r = 2.
......................................................................................
Okrąg o środku O(0, 0) i promieniu r = 2:
x2 + y2 = 4 ⇒ y = √4 − x2 lub y = −√4 − x2
W tym zadaniu występuje y = √4 − x2.
......................................................................................
Widać na rysunku, że linia prosta jest nad półokręgiem w przedziale (x1, x2).
Teraz możemy podnieść obustronnie do kwadratu nierówność x − 1 > √4 − x2
i rozwiązać ją, po uwzględnieniu dziedziny i sytuacji opisanej rysunkiem otrzymamy
odpowiedź podaną przez Marzenę i Tamarę.