<pomocy> wklęsłość, wypukłość i pkt przegięcia bib: Jak obliczyć wklęsłość, wypukłość i pkt przegięcia tej funkcji: y=e^{arc tgx}

Trivial: Trzeba policzyć drugą pochodną i sprawdzić kiedy jest większa od zera (wypukła), mniejsza od zera (wklęsła), równa zeru (punkt przegięcia).

bib: tylko że tutaj ta druga pochodna z tej funkcji wychodzi mi 0

Trivial: Pokaż jak liczysz.

bib: y'=e^{arc tgx}*(1/1+x²) y"= (e^{arc tgx}*(1/1+x²))*(1/1+x²)+(e^{arc tgx}*(−1/(1+x²)²)=e^{arc tgx}*((1/(1+x²)²)−(1/(1+x²)²)

Bogdan:

Trivial: Źle policzona druga pochodna. O tu ↑

Trivial:

	a
I da się pisać ułamki.		= U{a}{b}
	b

bib: to jak ma wyglądać ta pochodna bo ja licze i licze i ciagle mi wychodzi to samo chyba juz mi się myslenie wyłączyło

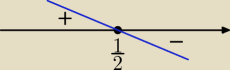
Bogdan: y = e^arctgx

	earctgx
y' =
	1 + x2

	earctgx   * (1 + x2) − 2xearctgx 1 + x2
y'' =		=
	(1 + x2)2

	1   −2earctgx(x − )   2
=
	(1 + x2)2

	1		1		1
f∪ dla x∊(−∞,		), f∩ dla x∊(		, +∞), punkt przegięcia yPP = f(		).
	2		2		2

Trivial:

	earctgx
y' =
	1+x2

Jeżeli już chcesz koniecznie liczyć ze wzoru na iloczyn (nie polecam) to tak:

	1		1
y'' = earctgx*		+ earctgx*(−		)*2x = ...
	(1+x2)2		(1+x2)2

Lepiej jednak ze wzoru na iloraz:

	1   earctgx* *(1+x2)−earctgx*2x   1+x2		1−2x
y'' =		=earctgx*		.
	(1+x2)2		(1+x2)2

Bogdan: a przy okazji − wklęsłości i wypukłości się nie oblicza,

bib: dziękuję bardzo. Myslałam że pochodna z ¹_1+x² to to samo co pochodna z (1+x²)⁻¹ czyli −(1+x²)⁻²czyli ⁻¹_(1+x²)²

Trivial: Bo to jest to samo, tyle że:

	2x
[(1+x2)−1]' = −1*(1+x2)−2*(1+x2)' = −		.
	(1+x2)2

bib: a ciągle zapominałam o tym 2x

kampo: hej mam prosbe. obliczyłam zadanie ale chciałabym mieć pewność czy jest dobrze: funckja f(x)=arctgx−x jest wklęsła na przedziale: i tu mi wyszlo (0; +∞) wypukła na przedziale : (−∞;0) mógłby ktoś sprawdzić czy na pewno dobrze;>