POMOCY xyz: Podstawą pewnego ostrosłupa o wierzchołku S jest kwadrat ABCD. Krawędź AS jest prostopadła do podstawy. Najdłuższa krawędź boczna ma długość 12 i tworzy z podstawą kąt o mierze 60 stopni. Oblicz objętość tego ostrosłupa.

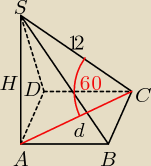
Ajtek: Δ ACS jest prostokątny o kątach 30^o, 60^o, 90^o czyli: d=6, H=6√2 P_p=¹₂d² V=P_p*H Podstawić, policzyć.

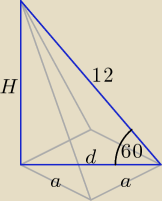
Bogdan: Oj Ajtek − trzeba poprawić Korzystając z własności trójkąta prostokątnego o kącie ostrym 60^o otrzymujemy:

	12
d =		= 6, H = d√3 = 6√3
	2

	1		1
Objętość V =		*		d2*H = ...
	3		2

Ajtek: No fakt, jak robiłem to zadanko, to jadłem obiad i ¹₃ też zjadłem. Swoją drogą to kwaśna ta ¹₃ . Dzięki Bogdan za zwrócenie ta to uwagi.

Bogdan:

trick: Dzięki bardzo