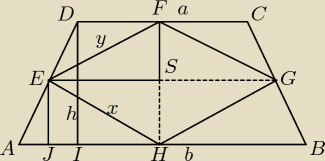
 Oznaczenia:a i b, długości krótszej i dłuższej podstawy
h − wysokość trapezu.
Celem jest: a) udowodnienie, że figura EHGF jest rombem
b) udowodnienie, że figura EHGF ma dwa razy mniejsze pole powierzchni niż sam trapez.
a)
Cechą charakterystyczną rombów jest to, że ich wszystkie boki mają taką samą długość. Nie
trzeba udowadniać, że |EH|=|HG|, gdyż rysunek jest symetryczny, więc jest to oczywiste. Należy
jednak udowodnić, że |EH|=|EF| (dla uproszczenia |EH|=x, |EF|=y)
Udowodnijmy więc, że x=y
Oznaczenia:a i b, długości krótszej i dłuższej podstawy
h − wysokość trapezu.
Celem jest: a) udowodnienie, że figura EHGF jest rombem
b) udowodnienie, że figura EHGF ma dwa razy mniejsze pole powierzchni niż sam trapez.
a)
Cechą charakterystyczną rombów jest to, że ich wszystkie boki mają taką samą długość. Nie
trzeba udowadniać, że |EH|=|HG|, gdyż rysunek jest symetryczny, więc jest to oczywiste. Należy
jednak udowodnić, że |EH|=|EF| (dla uproszczenia |EH|=x, |EF|=y)
Udowodnijmy więc, że x=y
| |EG| | ||
Z tw. Pitagorasa wynika, że y2=(|FS|)2+( | )2 | |
| 2 |
| a+b | ||
Wzór na |EG| wynika z własności trapezów i wyraża się tak: |EG|= | ||
| 2 |
| h | ||
|FS| zaś to nic innego jak połowa wysokości, czyli | ||
| 2 |
| b | ||
|AH|= | ||
| 2 |
| |AI| | ||
Z tw. Talesa wynika, że |AJ|=|JI|, lub też: | =|AJ| | |
| 2 |
| b−a | b−a | |||
|AI|= | => |AJ|= | |||
| 2 | 4 |
| b | b−a | |||
Czyli: |JH|= | − | |||
| 2 | 4 |
| |EG| | h | a+b | ||||
y2=(|FS|)2+( | )2=( | )2+( | )2 | |||
| 2 | 2 | 4 |
| h | b | b−a | ||||
x2=(|EJ|)2+(|JH|)2=( | )2+( | − | )2 | |||
| 2 | 2 | 4 |
| a+b | b | b−a | ||||
(x=y), muszą się sobie równać pozostałe składniki ( | = | − | ) | |||
| 4 | 2 | 4 |
| a+b | ||
L= | ||
| 4 |
| b | b−a | 2b−b+a | a+b | |||||
P= | − | = | = | |||||
| 2 | 4 | 4 | 4 |
| (a+b)*h | ||
Wzór na pole trapezu, powszechnie znany i stosowany: Pt= | ||
| 2 |
| |EG|*|FH| | ||
Pr= | ||
| 2 |
| a+b | ||
Jak już wcześniej zostało wykazane, |EG|= | , a przekątna |FH| pokrywa się z wysokością | |
| 2 |
| |EG|*|FH| |
| (a+b)*h | ||||||||||
Pr= | = | = | ||||||||||
| 2 | 2 | 4 |