Planimetria
Ernest:
Podstawą ostrosłupa ABCDS jest kwadrat ABCD o boku długości 4.
Odcinek DS jest wysokością ostrosłupa i ma długość 6.
Punkt M jest środkiem odcinka DS.
Oblicz pole przekroju ostrosłupa płaszczyzną BCM.
20 lut 09:21
ICSP: 2
√34
20 lut 10:35
Ajtek:
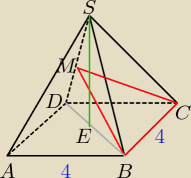
Jak dla mnie w treści zadania jest błąd.
DS nie może być wysokością ostrosłupa, gdyż jest jego krawędzią boczną.
Nawet po uwzględnieniu tej poprawki, nie mam pomysłu jak to ugryźć.
20 lut 13:52
Trivial:
Czemu nie?
20 lut 13:53
Ajtek: Totalna pustka w głowie po sobocie
.
20 lut 14:02
dero2005:
ostrosłup nie jest prawidlowy
20 lut 14:26
Ajtek: Toż piszę, że mi jeszcze głowa nie pracuje
.
Wszystko jasne.
20 lut 14:31
dero2005:
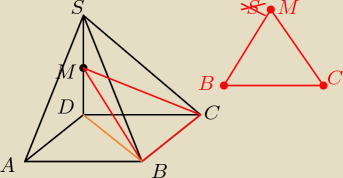
DS = 6
BC = 4
DM = 3
BD = AB
√2 = 4
√2
BM =
√(DM)2+(DB)2 =
√32+(4√2)2 =
√41
CM =
√(DM)2+(DC)2 =
√25 = 5
mamy trójkąt o bokach dlugości
4 cm, 5 cm i
√41 cm policzyć jego pole i koniec
20 lut 16:11
s: jest blad poniewaz z przekroju powstaje trapez a nie trojkat, do przekroju trzeba dodac pkt
lezacy w polowie AS
7 kwi 19:16
Mila: Zgadzam się z S, u obydwu Panów przekrój jest błędnie narysowany.
7 kwi 19:37
Mila:
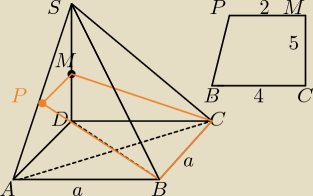
Przekrój BCMP jest trapezem prostokątnym.
DM=3, a=4
MC
2=3
2+4
2
MC=5
PM jest odcinkiem łączącym środki boków ΔADs, zatem jest równy połowie podstawy AD.
PM=2
P
BCMP=15J
2
7 kwi 20:45
IoIek: Czemu?
29 kwi 19:03