Gustlik: A= (−2, −2),
B= (1, 1),
C= (−3, 3)
Do tego potrzebne są współrzędne czwartego wierzchołka D.
Najpierw znajduję równanie podstawy AB:
| | yB−yA | | 1−(−2) | | 3 | |
a= |
| = |
| = |
| =1
|
| | xB−xA | | 1−(−2) | | 3 | |
Podstawa AB ma równanie:
y=x+b
Podstawiam wspólrzędne punktu B:
1=1+b
b=0
Podstawa ma równanie y=x.
Znajduję równanie symetralnej AB − jest to jednocześnie symetralna "górnej" podstawy CD.
| | xA+xB | | yA+yB | | −2+1 | | −2+1 | | 1 | | 1 | |
SAB=( |
| , |
| =( |
| , |
| )=(− |
| , − |
| )
|
| | 2 | | 2 | | 2 | | 2 | | 2 | | 2 | |
| | 1 | |
Symetralna ma równanie y=−x+b (a2=− |
| warunek prostopadłości) i przechodzi przez |
| | a1 | |
S
AB.
Zatem
b=−1
Równanie symetralnej y=−x−1
Znajduję równanie "górnej" podstawy CD jako prostej równoległej do AB i przechodzącej przez
punkt C.
y=x+b (a
2=a
1 − warunek równoległości)
Podstawiam punkt C:
3=−3+b
b=6
Podstawa CD ma równanie y=x+6.
Znajduję współrzędne środka "górnej" podstawy S
CD z układu równań:
{ y=−x−1 (symetralna)
{ y=x+6 (podstawa CD)
−x−1=x+6
−2x=7 /:(−2)
Liczę współrzędne środka S
CD ze wzoru:
| | xC+xD | | yC+yD | | −3+x | | 3+y | |
SCD=( |
| , |
| )=( |
| , |
| ) i porównuję z obliczonymi |
| | 2 | | 2 | | 2 | | 2 | |
wcześniej:
−3+x=−7
x=−7+3
x=−4
3+y=5
y=5−3
y=2
Zatem D=(−4, 2)
Wierzchołki trapezu maja współrzędne:
A= (−2, −2),
B= (1, 1),
C= (−3, 3)
D=(−4, 2)
Aby obliczyć pole wyprowadzam wektory z jednego z wierzchołków, np. z A do wszystkich
pozostałych wierzchołków i dzielę trapez na dwa trójkąty ABC i ACD.
Liczę współrzędne tych wektorów:
AB
→=B−A=[1−(−2), 1−(−2)]=[3, 3]
AC
→=C−A=[−3−(−2). 3−(−2)]=[−1, 5]
AD
→=D−A=[−4−(−2), 2−(−2)]=[−2, 4]
Pole ΔABC:
Liczę wyznacznik wektorów AB
→ i AC
→:
d(AB
→, AC
→)=
| 3 3 |
| −1 5 |
=3*5−3*(−1)=15+3=18
| | 1 | | 1 | |
Pole ΔABC= |
| |d(AB→, AC→)|= |
| *|18|=9
|
| | 2 | | 2 | |
Liczę pole ΔACD w podobny sposób:
Wyznacznik wektorów AC
→ i AD
→:
d(AC
→, AD
→)=
| −1 5 |
| −2 4 |
=(−1)*4−5*(−2)=−4+10=6
| | 1 | | 1 | |
Pole ΔACD= |
| |d(AC→, AD→)|= |
| *|6|=3
|
| | 2 | | 2 | |
Pole trapezu = pole ΔABC + pole ΔACD =9+3=12.
Licze obwód tego trapezu:
AB
→=[3, 3] − podstawa, dł. |AB|=
√32+32=
√9+9=
√18=3
√2
AD
→=[−2, 4] − "lewe" ramię dł. |AD|=
√(−2)2+42=
√4+16=
√20=2
√5
Wierzchołki:
A= (−2, −2),
B= (1, 1),
C= (−3, 3)
D=(−4, 2)
Liczę współrzedne "górnej" podstawy CD
→=[−4−(−3), 2−3]=[−1, −1] oraz jej długość:
|CD|=
√(−1)2+(−1)2=
√2
Liczę współrzedne "prawego" ramienia oraz jego długość:
BC
→=[−3−1, 3−1]=[−4, 2]
|BC|=
√(−4)2+22=
√16+4=
√20=2
√5
Obwód=|AB|+|BC|+|CD|+|AD|=3
√2+2
√5+
√2+2
√5=4p{2]+4
√5.
Gustlik: Równanie kierunkowe prostej, czyli zwykła funkcja liniowa:
y=ax+b
Współczynnik kierunkowy prostej przechodzącej przez dwa punkty:
| | yB−yA | |
a= |
| − najprostszy sposób wyznaczania prostej przechodzącej przez dwa punkty, |
| | xB−xA | |
obliczyłem współczynnik tym wzorem, wyszło a=1, potem wstawilem do równania prostej y=ax+b,
stąd y=x+b. Potem trzeba wstawić do równania współrzędje jednego z tych punktów A lub B aby
obliczyć b, ja wstawiłem punkt B.
Symetralną obliczyłem z warunku prostopadłości prostych. Zależność między współczynnikami
| | 1 | | 1 | |
kierunkowymi prostych prostopadłych wygląda tak: a2=− |
| , czyli a2=− |
| =−1, stąd |
| | a1 | | 1 | |
wyszlo y=−x+b. Wstawiłem współrzędne środka S
AB, żeby obliczyć b.
Wyjasnienie do wektorowej metody obliczania pól trójkątów i innych figur masz tutaj:
https://matematykaszkolna.pl/forum/forum.py?komentarzdo=i18 .
Wiem, że wielu z tych wzorów nie ma omawianych w szkole, bo debile w MEN tak ułożyli program, a
nauczyciele nie wiem czemu nie chcą ich pokazywać, ale ja lubię proste metody i minimum
układów równań. Pozdrawiam
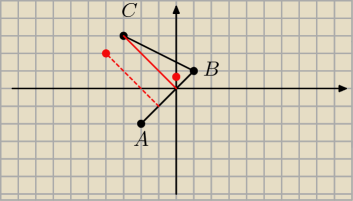lub graficznie...
A = (−2, −2)
B = (1, 1)
C = (−3, 3)
wysokość opada na ładny równy punkt. ponieważ jest to trapez równoramienny to z drugiej strony
wysokość będzie opadać symetrycznie.
Czyli D = (−4, 2)