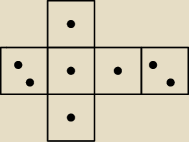
Jak to obliczyć? MuBay: Jak to obliczyć za pomocą omegi? Doświedczenie losowe polega na dwukrotnym rzucie symetryczną kostką sześcienną, której siatkę przedstawia rysunek. Oblicz prawdopodobieństwo a. zdarzenia A, że uzyskano w obu rzutach ten sam wynik b. zdarzenia B, że uzyskany iloczyn oczek jest liczbą parzystą

Basia: Ω= { (1,1) (1,2) (2,1) (2,2) } ale te zdarzenia nie są jednakowo prawdopodobne P(1,1) = ⁴₆*⁴₆ = ²₃*²₃ = ⁴₉ P(1,2) = ⁴₆*²₆ = ²₃*¹₃ = ²₉ P(2,1) = ²₆*⁴₆ = ¹₃*²₃ = ²₉ P(2,2) = ²₆*²₆ = ¹₃*¹₃ = ¹₉ A = {(1,1) (2,2)} P(A) = ⁴₉+¹₉ = ⁵₉ B = {(1,2) (2,1) (2,2)} P(B) = ²₉+²₉+¹₉ = ⁵₉

Basia: można też tak: 1₁ − "jedynka" na ściance pierwszej 1₂ − "jedynka" na ściance drugiej 1₃ − "jedynka" na ściance trzeciej 1₄ − "jedynka" na ściance czwartej 2₅ − "dwójka" na ściance piątej 2₆ − "dwójka" na ściance szóstej Ω= {(1₁, 1₁) (1₁,1₂) (1₁,1₃) (1₁,1₄) (1₁,2₅) (1₁,2₆) (1₂, 1₁) (1₂,1₂) (1₂,1₃) (1₂,1₄) (1₂,2₅) (1₁,2₆) .............................................................. (2₆, 1₁) (2₆,1₂) (2₆,1₃) (2₆,1₄) (2₆,2₅) (2₆,2₆)} przy takim podejściu masz 36 jednakowo prawdopodobnych zdarzeń elementarnych no i teraz liczysz te, które sprzyjają A (jest ich 20) i te, które sprzyjają B (też 20)

Sandra: 4*1+2+6*−1

Sandra: oblicz te działanieeee bo mi cos nie wychodzii wynik wyszedł mi 12*2