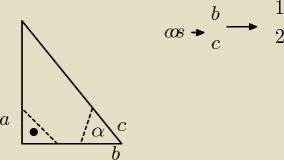Kąt α jest ostry, cosα= 12.
Oblicz √tg2α−1
| a | √3b | |||
tgα= | = | =U{√3} | ||
| b | b |
| sinx | ||
z jedynki tryg obliczasz sinusia sin>0 bo I cwiartka i z rownania tgx= |  | |
| cosx |
| 1 | ||
cosα = | ||
| 2 |
| 1 | ||
sin2α = 1 − ( | )2 | |
| 2 |
| 1 | ||
sin2α = 1 − | ||
| 4 |
| 3 | ||
sin2α = | ||
| 4 |
| √3 | √3 | |||
sinα = | ⋁ sinα = | <− nie spełnia zał. zadania, bo α jest | ||
| 2 | 2 |
| sinα |
| √3 | 2 | |||||||||||
tgα = | = | = | * | = √3 | ||||||||||
| cosα |
| 2 | 1 |
| 1 | ||
jeśli cosα = | , to α = 60 stopni,
| |
| 2 |
Jacek jak ja na to nie wpadłem