Zadanie z parametrem
Ejczwentura: Określ liczbę rozwiązań równania |x
2−6x+5|+m−2=0. Chciałbym to zrobić bez rysowania wykresu.
Napisze tutaj swoje rozwiązanie powiedzcie co robię źle.
Założenia:
x
2−6x+5 ≥ 0 lub x
2−6x+5 < 0, x
1+x
2 >0, x
1*x
2 > 0, Δ>0
1.x
2−6x+5 ≥ 0
x
2−6x+3+m=0
Δ = 24−4m
24−4m >0
m<6
x
1*x
2 = 3+m
m>−3
x
1+x
2 = 6
6 > 0
Podsumowanie −−−−> (−
∞;6), (−3;
∞)
2. x
2−6x+5 < 0
−x
2+6x−7+m=0
Δ = 4m+8
m>−2
x
1*x
2 = 7−m > 0
m< 7
x
1+x
2 = −6
−6 > 0
Podsumowanie −−−> Sprzeczne
Ostatecznie: (−
∞;6)n(−3;
∞)
m∊ (−3;6)
Wynik się nie zgadza co robię źle(Jak nie wszystko
)?
18 lut 22:29
Godzio:
No dobra ale musisz sprawdzić ten przedział, x
2 − 6x + 5 ≥ 0 ⇒ x ∊ ... i te m musi sie w nim
zawierać
4 razy więcej roboty niż z rysowaniem i po co w ogóle warunki x
1 + x
2 czy x
1 *
x
2 ?
18 lut 22:47
Ejczwentura: no bo w poleceniu jest ma dokładnie dwa rozwiązania dodatnie
18 lut 22:50
Godzio:
No to roboty że cho cho
Chcesz mogę pokazać jak to zrobić ale nie gwarantuje że na 100%
będzie dobrze, algebraicznie może być ciężko
18 lut 22:51
Ejczwentura: mozesz zrobić był bym wdzięczny ale skoro mówisz że graficznie lepiej to zrób graficznie
18 lut 22:53
Godzio:
Zrobię tak i tak
18 lut 22:55
Godzio:
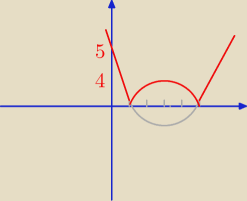
|x
2 − 6x + 5| = 2 − m
2 dodatnie rozwiązania są dla
5 ≥ 2 − m > 4 / − 2
3 ≥ −m > 2 /*(−1)
−3 ≤ m < −2
Odp: m ∊ <−3,−2)
Męczę się algebraicznie ale nie wiem co z tego wyjdzie
18 lut 23:18
Godzio:
Podaj jeszcze raz treść całą, bo nie wiem co właściwie mam liczyć ilość dodatnich rozwiązań ze
względu na parametr m ? bo jeśli tak to w tym z wykresem
4 rozwiązania dodatnie są dla
0 < 2 − m < 4
3 rozwiązania dodatnie dla:
2 − m = 4
18 lut 23:21
Ejczwentura: Podaj wszystkie wartości parametru m dla których powyższe równanie ma dokłądnie dwa dodatnie
rozwiązania
18 lut 23:25
Ejczwentura: I jak tam
?
19 lut 00:00