planimetria :\ lenul: Kąt ostry równoległoboku ma miarę 60 stopni. Stosunek kwadratów długości przekątnych jest równy

	1
		. Wykaż, że ten równoległobok jest rombem.
	3

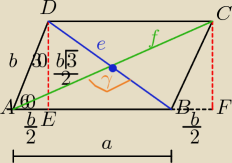Eta: Podaję jeden ze sposobów Bogdan zapewne za moment poda drugi sposób

e2		1
	=
f2		3

f²= 3e² => f= e√3

	e*f
P= a*h i P=		*sinγ
	2

z ΔAED

	b√3
h=
	2

	b
i |AE|=
	2

Wykażemy,że jeżeli |<γ |= 90^o to równoległobok jest rombem

	ab√3
P=
	2

z tw. Pitagorasa w trójkątach: BED i AFC

	b2
h2= e2−(a−b2)2 = e2−a2+ab−
	4

	b2
h2= f2− (a +b2)2= f2−a2 −ab −
	4

	b2		b2
f2−a2−ab −		= e2−a2+ab −
	4		4

3e²−e²= 2ab => e²= ab porównując z wzoróww na pole mamy:

	e*f		ab√3
		*sinγ=
	2		2

e2√3		ab√3
	*sinγ=
2		2

	ab√3		ab√3
		*sinγ=
	2		2

sinγ= 1 => γ= 90^o zatem równoległobok jest rombem c.n.u