czy jest tu jakis kozak Pawson: zadanie dla kozaka znajdź ekstrema funkcji

	x		2
zad.1.f(x)=		+
	2		x

	2x+1
zad.2.f(x)=
	x−4

	x3
zad.3.f(x)=
	(x−1)2

zad.4.f(x)=x√4x−x² zad.5.f(x)=(x−5)e^x

Godzio: A z czym masz problem ? Wyznaczenie pochodnej ? Rozwiązaniem równania f'(x) = 0 ? Czy sprawdzeniu czy dany punkt jest ekstremum ?

Pawson: przede wszystkim wykres i sprawdzenie czy dany punkt jest ekstremum

Godzio: Mogę zrobić 2 przykłady, wybierz to pokaże jak to zrobić

Pawson: 2,4 z góry dziekuję

Godzio: 2. D = R − {4}

	2x + 1
f(x) =
	x − 4

	2(x − 4) − (2x + 1)		2x − 4 − 2x + 1		−3
f'(x) =		=		=
	(x − 4)2		(x − 4)2		(x − 4)2

	−3
f'(x) = 0 ⇒		= 0 ⇒ −3 = 0 −− sprzeczność brak ekstremum
	(x − 4)2

4. 4x − x² ≥ 0 ⇒ x(4 − x) ≥ 0 ⇒ D = <0,4> f(x) = x√4x − x²

	1		2x − x2
f'(x) = √4x−x2 + x*		* (4 − 2x) = √4x − x2 +		=
	2√4x − x2		√4x − x2

	4x − x2 + 2x − x2		−2x2 + 6x
=		=
	√4x − x2		√4x − x2

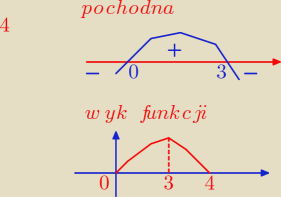
f'(x) > 0 ⇒ −2x² + 6x > 0 ⇒ −2x(x − 3) > 0 ⇒ x ∊ (0,3) −− funkcja rośnie f'(x) < 0 ⇒ x ∊ (3,4) −− funkcja maleje x = 0 ⇒ f(0) = 0 (0,0) − minimum x = 3 ⇒ f(3) = 3√12 − 9 = 3√3 (3,3√3) − maksimum x = 4 ⇒ f(4) = 0 (0,4) − minimum lokalne

karol: w drugim zadaniu juz wiem dlaczego nie ma ekstremum ale pochodna wychodzi mi troche inaczej zamiast −3 powinno być −7 czy sie myle?

Godzio: Zgadza się, 2 * (−4) = −8