| 2 | ||
wysokość tego ostrosłupa jest równa 5 | cm, oblicz cosinus kąta nachylenia krawędzi | |
| 3 |
| 15 | ||
niestety wynik wyszedł mi zgoła odmienny od tego, co sugeruje książka(czyli | )
| |
| 17 |
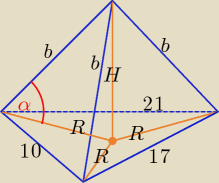Z treści zadania wynika, że wszystkie krawędzie boczne ostrosłupa są równej długości,
a to oznacza, że spodek wysokości ostrosłupa znajduje się w środku okręgu opisanego
na podstawie ostrosłupa.
| 17 | ||
H = | ||
| 3 |
| R | 10*17*21 | |||
cosα = | , R = | , b = √H2 + R2 | ||
| b | 4*PΔ |
| 10 + 17 + 21 | ||
Pole trójkąta PΔ = √ p * (p − 10) * (p − 17) * (p − 21) , p = | ||
| 2 |
| 15 | ||
Liczby są starannie dobrane w zadaniu, cosα = | . | |
| 17 |
