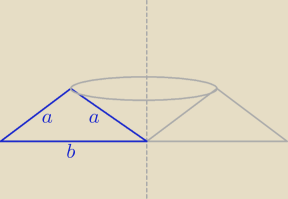
Mam problem, za nic nie mogę sobie wyobrazić co powstanie przez obrót trójkąta równoramiennego
(tak jak na rysunku)
Jak zapisać objętość czegoś takiego ?
Dzięki
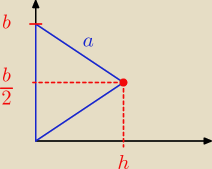h = √a2 + (12b)2
Objętość można policzyć na przykład tak:
Jako że nie chce mi się myśleć zrobię z całek.
| b | ||
1. Wyznaczamy wzór prostej przechodzącej przez punkty (0, b) i (h, | ). | |
| 2 |
| b | ||
2. Wyznaczamy wzór prostej przechodzącej przez punkty (0, 0) i (h, | ). | |
| 2 |
| b | ||
= Ah + b | ||
| 2 |
| b | ||
A = − | ||
| 2h |
| b | ||
(1) k: y = − | x + b | |
| 2h |
| b | ||
(2) l: y = | x | |
| 2h |
| b | b | |||
V = π∫0h[(− | x + b)2 − ( | x)2]dx | ||
| 2h | 2h |
| b2 | ||
V = π∫0h(− | x + b2)dx | |
| h |
| b2 | h2 | b2h | ||||
V = π(− | * | + b2h) = π | . | |||
| h | 2 | 2 |
h = √a2 − (12b)2
A zaraz się biorę za wyprowadzenie tego wzoru co raczej nie będzie trudne
Czy dobrze to Ci nie powiem bo odpowiedzi nie mam, ale jak zrobię tym sprawdzonym sposobem to
Ci potwierdzę
| 1 | ||
Vściętego = | πH(R2 + Rr + r2) | |
| 3 |
| 1 | ||
Vwyciętego stożka = | πr2H | |
| 3 |
| 1 | 1 | |||
Vś − Vw = | πH(R2 + Rr) H = 2√4a2 − b2 R = b, r = | b | ||
| 3 | 2 |
| 2 | 1 | 2 | 3 | |||||
V = | π√4a2 − b2 * (b2 + | b2) = | π√4a2 − b2 * | b2 = | ||||
| 3 | 2 | 3 | 2 |
V = πb2√4a2 − b2
| b2h | |
π skoro h = 2√4a2 − b2 to po podstawieniu 2 się skrócą i zostanie | |
| 2 |