Graniastosłupy proszę o pomoc. Piotr: Dłuższa przekątna graniastosłupa prawidłowego sześciokątnego o długości 12 cm jest nachylona do płaszczyzny podstawy pod kątem 35stopni. Jaką długość ma krótsza przekątna tego graniastosłupa, Jaki kąt tworzy ona z płaszczyzną podstawy. Proszę o wytłumaczenie zadania. z góry dziękuje i pozdrawiam.

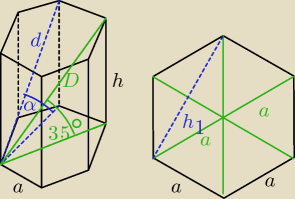
dero2005: D = 12 cm − dłuższa przekątna ^h_D = sin 35° = 0,5735 h = D* sin 35° = 12* 0,5735 = 6,88 cm → wysokość graniastosłupa ^2a_D = cos 35° = 0,8192 2a = D* cos 35° = 12* 0,8192 = 9,83 cm a = ^2a₂ = ^9,83₂ = 4,92 cm h₁ = ^a√3₂ = ^4,92*√3₂ = 4,26 cm d = √h² + (2h₁)² = √6,88² + 8,52² = √119,92 = 10,95 cm → przekątna krótsza sin α = ^h_d = ^6,88_10,95 = 0,6283 α = 38°55'32'' → kąt krótszej przekątnej z podstawą