Oblicz pole powierzchni bocznej ostrosłupa
karol: Podstawą ostrosłupa czworokątnego ABCDS jest kwadrat ABCD. Pole trójkąta równoramiennego ACS
jest równe 120 oraz IACI:IASI=10:13. Oblicz pole powierzchni bocznej tego ostrosłupa.
16 lut 11:06
Niunia85:
pole powierzchni bocznej to jest suma pól trójkątów skoro pole trójkąta jest 120 a tych
trójkątów jest 4 to PPB=4*120=480
może tutaj coś innego trzeba policzyć?
16 lut 11:20
R.W.17l:
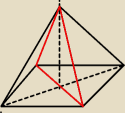
Nie wiem czy zauważyłęś, ale pole CZERWONEGO trójkąta jest równe 120
16 lut 11:25
R.W.17l: *aś
16 lut 11:27
R.W.17l:
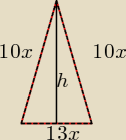
Liczysz h, potem z pola liczysz x
następnie liczysz ile wynosi bok podstawy, wiedząc, że 13x to przekątna
Potem już prosto, bo masz 4 trójkąty o bokach BokPodstawy:10x:10x
16 lut 11:41
karol: coś mi nie wychodzi w obliczeniach
HELP ME
16 lut 23:13
Gustlik: R.W.17l Chyba masz czseki błąd − AC to podstawa i jest równa 10x, a AS − to krawędź boczna i
jest równa 13x.
Natomiast metoda rozumowania poprawna.
Liczę h na "x"−ach z twierdzenia Pitagorasa:
(13x)
2=(5x)
2+h
2
169x
2=25x
2+h
2
h
2=144x
2 /
√
h=12x
Liczę pole na "x"−ach"
Ale pole P=120, więc
60x
2=120 /:60
x
2=2 /
√
x=
√2
Czyli przekatna podstawy − kwadratu : 10x=10
√2
Liczę krawędź podstawy
a
√2=10
√2
a=10
Liczę wysokość ostrosłupa:
h=12x=12
√2
Liczę wysokość ściany bocznej:
h
b2=5
2+(12
√2)
2
h
b2=25+144*2
h
b2=25+288
h
b=313 /
√
h
b=
√313
Pole boczne ostrosłupa prawidłowego − korzystam ze wzoru:
| | 1 | |
Pb= |
| L*hb, L − obwód podstawy, hb − wysokość ściany bocznej:
|
| | 2 | |
L=4a=4*10=40
17 lut 00:44
R>W.17l: Przepraszam za błąd, dziękuję za potwierdzenie słuszności mojej metody
17 lut 11:48
ΔΩ∞≤≥πδ: πΩπβαγδπΔΩ∞≤≥πδ
18 lut 22:43