... Fiolka: Zad2. Dla jakich wartości parametru m oba miejsca zerowe funkcji f(x)=x²+(2m−4)x+2m+1 są wieksze od −3?

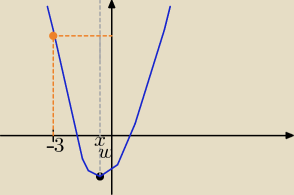
Eta: parametr "m" musi spełniać układ warunków: { Δ>0 { f(−3) >0 { x_w > −3

Wojtek: Δ= (2m−4)² − 4(2m+1) = 4m²−24m+12 4m² − 24m + 12 > 0 m²−6m+3 >0 Δm = 6² − 4*3 = 24 √Δm = 2√6 m₁ = (6−2√6)/2 = 3 − 2√6 m₂ = (6+2√6)/2 = 3 + 2√6 f(−3) = 9 + (2m−4)*(−3) + 2m + 1= 9 −6m + 12 + 2m + 1 = 22 − 4m 22 − 4m >0 m < 5,5 xw = −(2m−4)/2 = 2 − m 2 − m > 0 m < 2 m∊(3−2√6,2)

fdsf: Wojtek zapomniałeś w m₁ i m₂ o skróceniu z mianownikiem przy √6