bryły obrotowe zadania dla mistrzów michał: 1. Koło o średnicy 8 cm podzielono na połowy, z których wykonano dwie powierzchnie boczne stożków i połączono je podstawami. Oblicz objętość i pole całkowite otrzymanej bryły. 2. Oblicz objętość bryły powstałej w wyniku obrotu rombu o kącie ostrym 60⁰ i boku równym 8cm wokół: a) dłuższej przekątnej rombu, b) krótszej przekątnej rombu. 3. W kulę o promieniu R=2√13 wpisano walec, w którym stosunek długości promienia podstawy do wysokości jest równy 3:4. Oblicz pole powierzchni całkowitej i objętość walca.

michał: pomożecie, no to mi tylko rysunki zróbcie a ja sam skończe

dero2005: zad 1 P_c = π*8² = 64π cm² πl = 2πr r = ^l₂ = 4 h = √l² − r² = √48 = 4√3 V = ²₃πr²*h = ²₃π*4²*4√3 = ^128*π₃√3 cm³

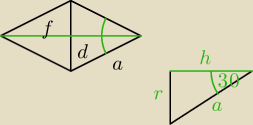
dero2005: r − promień stożka r = a sin 30 = 8* ¹₂ = 4 h − wysokość stożka h = √a²−r² = √64−16 = √48 = 4√3 V = ²₃πr²*h = ²₃π*4²*4√3 = ¹²⁸₃π√3 cm³ → objętość bryły powstałej przez obrócenie rombu wokół dłuższej przekątnej

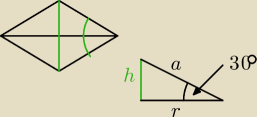
dero2005: r − promień stożka h − wysokość stożka a = 8 h = a sin 30 = 8 * ¹₂ = 4 r = √a²−h² = √64−16 =√48 = 4√3 V = ²₃πr²*h = 128π cm ³ → objętość bryły powstałej przez obrót rombu wokół dłuższej przekątnej

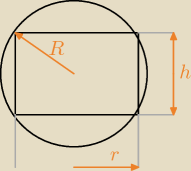
dero2005: zad 3 R = 2√13 ^r_h = ³₄ r = ³₄h R² = h² + (2r)² R² = ¹³₄h² h² = 16 h = 4 r = ³₄*4 = 3 V = πr²*h = 36π cm³ P_c = 2πr² + 2πr*h = 2πr(r+h) = 2π*4(3+4) = 56π cm²

dero2005: poprawka do zad 3) powinno być od czwartego wiersza (2R)² = h² + (2r)² h² = 64 h = 8 r = 6 V = 288π cm³ P_c = 768 cm²

miszcz: zad 1 Pc = π*82 = 64π cm2 πl = 2πr r = l2 = 4 h = √l2 − r2 = √48 = 4√3 V = 23πr2*h = 23π*42*4√3 = 128*π3√3 cm3