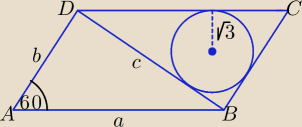
obliczyc dlugosci bokow i pole rownolegloboku strapiona:(: punkty A, B, C, D są kolejnymi wierzchołkami równolegloboku o obwodzie równym 26. wiedzac, że miara kata ABC wynosi 120 stopni i promień okregu wpisanego w trójkąt BCD jest równy √3 , oblicz długosci boków i pole tego równolegloboku.

Spike: A w odpowiedziach co jest?

strapiona:(: niestety problem w tym ze nie mam odp... ale gdybys mogł mnie chociaz naprowadzic, na sposob rozwiazania tego zadania to bylabym bardzo wdzieczna

Spike: A więc po kolei. Załączam link, tylko rysunek robiony na szybkiego w paincie żeby coś było do tłumaczenia Po podpisaniu boków i podzieleniu równoległoboku na 2 trójkąty, trzeba zauważyć, że są to trójkąty 30*/60*/90*, więc jeżeli bok 30*-60* nazwę a, to bok 60*-90* (BC)= 1/2a, a wysokość h=a√3/2 Obw= 2a + 2b= 2a+ 2* 1/2a=3a 26=3a /:3 a=26/3 h=(26/3*√3)/2 h=(26/3*√3)*1/2 h=26/6*√3 P_{obu trójkątów}=2*1/2*26/6*√3*26/6 P_{obu trójkątów}=26/6*√3*26/6 P_{obu trójkątów}=676/32*√3 P_{obu trójkątów}=21,125*√3 cm²=Pole równoległoboku Ps. Nie wiem po co dany był promień okręgu wpisanego. Może jakaś prostsza metoda, ale jesli już to ja jej nie widziałem

Spike: Zaraz link wstawię. Tylko obrazek się wyśle, a teraz coś się u dostawcy netu zrypało i bez proxy mam ustawioną przeglądarkę żeby mi net w ogóle chodził. 3 min

Spike: http://wyslijplik.pl/download.php?sid=CooANpT9

strapiona:(: dziekuje serdecznie kolego mam nadzieje ze wszystko bedzie dla mnie zrozumiale, ale bede nad tym jutro siedziec Milo, że jest takie forum ratujecie zycie

Wariacik: Wszystko super, tylko ze to jest zle rozwiazanie −,−

Bogdan: Wariacik ma rację. Podaję rozwiązanie 2a + 2b = 26 ⇒ a + b = 13 ⇒ (a + b)² = 13² ⇒ a² + b² = 169 − 2ab Pole trójkąta ABC i BCD:

	a + b + c		13 + c		1		ab√3
PΔ =		*√3 =		*√3 i PΔ =		absin60o =
	2		2		2		4

13 + c		ab√3
	*√3 =		/*4 ⇒ 26 + 2c = ab
2		4

Z twierdzenia cosinusów w trójkącie ABC: c² = a² + b² − 2abcos60^o ⇒ c² = 169 − 2ab − ab ⇒ c² = 169 − 3(26 + 2c) c² = 169 − 78 − 6c ⇒ c² + 6c − 91 = 0 ⇒ (c − 7)(c + 13) = 0 i c>0 ⇒ c = 7 ab = 26 + 2*7 = 40

	√3
Pole równoległoboku P = absin60o = 40*		= 20√3
	2

Długości boków obliczymy rozwiązując układ równań: a + b = 13 i ab = 40, a, b > 0. Po rozwiązaniu otrzymujemy: (a = 5 i b = 8) lub (a = 8 i b = 5)