trójkąt równoboczny ziomek: mam do was pytanie ,jak to jest z dzieleniem się wysokości w trójkącie równobocznym?

	1		2
kiedy w zadaniu możemy poznać że należy podstawić		a kiedy
	3		3

na przykładzie tego zadania https://matematykaszkolna.pl/strona/1888.html . (od momentu kiedy zaczyna się liczenie h_p)

	1		2
Jak zajarzyć który ułamek wstawić		czy		/po czym poznać?
	3		3

Czytałem https://matematykaszkolna.pl/strona/856.html, ale dalej nie wiem.

Bogdan: Długość R promienia okręgu opisanego na trójkącie równobocznym

	1		2
R =		a√3 =		h = 2r
	3		3

Długość r promienia okręgu wpisanego w trójkąt równoboczny

	1		1		1
r =		a√3 =		h =		R
	6		3		2

ziomek: Jak dobrze rozumiem to jest wyprowadzenie wzoru na stosunek długości na jaki sie dzieli wysokość w trójkącie równoramiennym. Hmm...nie do końca o to mi chodziło,mi nawet nie chodzi o wyprowadzenie wzoru ani skąd to się wzięło ,bo to ogarniam. Mi chodzi o coś bardziej elementarnego Mam sobie zadanie https://matematykaszkolna.pl/strona/1888.html

	2
czytam zadanie i dochodzę do momentu w którym mam x=		hp itd potrzebuje to liczyć żeby
	3

wyliczyć ile jest równe "a" czyli długość boku trójkąta równobocznego . Tu już nie wiem po czym się połapać że to akurat ma być 2/3h_p a nie 1/3h_p.

	1		2
Od tego momentu po prostu nie wiem czy mam wstawiać		h czy		h tak jak jest w tym
	3		3

akurat zadaniu, chcem tylko poznać jakiś patent dzięki czemu mogę się zorientować czy mam wstawiać 1/3h czy 2/3h.

Bogdan: W tym zadaniu niepotrzebna jest wysokość trójkąta równobocznego. Zaraz pokażę.

Bogdan:

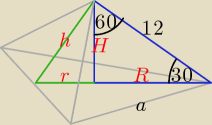
	1
R =		a√3 / * √3 ⇒ a = R√3,
	3

Korzystamy z własności trójkąta prostokątnego o katach ostrych 30^o i 60^o.

	1
H =		* 12 = 6, R = H√3 = 6√3, a = 6√3*√3 = 18,
	2

	1		1
r =		R =		*6√3 = 3√3, h = √H2 + r2 = ...
	2		2

ziomek: przeanalizowałem to co Pan napisał teraz i nareszcie zrozumiałem, dziękuje

Bogdan: